
在数列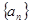 中,如果存在常数
中,如果存在常数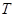
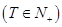 ,使得
,使得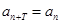 对于任意正整数
对于任意正整数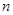 均成立,那么就称数列
均成立,那么就称数列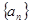 为周期数列,其中
为周期数列,其中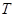 叫做数列
叫做数列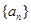 的周期. 已知数列
的周期. 已知数列 满足
满足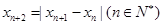 ,若
,若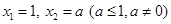 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前2012项的和
的前2012项的和 为( )
为( )
| A.1339+a | B.1340+a | C.1341+a | D.1342+a |
科目:高中数学 来源: 题型:单选题
在2000年至2003年期间,甲每年6月1日都到银行存入 元的一年定期储蓄,若年利率为
元的一年定期储蓄,若年利率为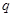 保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
保持不变,且每年到期的存款本息自动转为新的一年定期,到2004年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
A.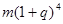 元 元 | B.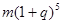 元 元 |
C.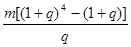 元 元 | D. 元 元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设数列{an}中,若an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”,已知数列{bn}为“凸数列”,且b1=1,b2=-2,则数列{bn}的前2014项和为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com