
【题目】已知函数f(x)=m﹣ ![]()
(1)若f(x)是R上的奇函数,求m的值
(2)用定义证明f(x)在R上单调递增
(3)若f(x)值域为D,且D[﹣3,1],求m的取值范围.
【答案】
(1)解:∵f(x)是R上的奇函数,
∴f(x)+f(﹣x)=m﹣ ![]() +m﹣
+m﹣ ![]() =0,
=0,
即2m﹣( ![]() +
+ ![]() )=02m﹣1=0,
)=02m﹣1=0,
解得m= ![]()
(2)解:设 x1<x2且x1,x2∈R,
则f(x1)﹣f(x2)=m﹣ ![]() ﹣(m﹣
﹣(m﹣ ![]() )=
)= ![]() ,
,
∵x1<x2∴ ![]() ,
, ![]()
![]() ,
,
∴f(x1)﹣f(x2)<0,
即f(x1)<f(x2),
∴f(x)在R上单调递增
(3)解:由 ![]() ,所以m﹣1<f(x)<m,f(x)值域为D,且D[﹣3,1],
,所以m﹣1<f(x)<m,f(x)值域为D,且D[﹣3,1],
∴D=(m﹣1,m),
∵D[﹣3,1],
∴ ![]() ,
,
∴m的取值范围是[﹣2,1]
【解析】(1)由奇函数的定义可得f(x)+f(﹣x)=0恒成立,由此可求得m值;(2)设 x1<x2且x1 , x2∈R,利用作差证明f(x1)<f(x2)即可;(3)先根据反比例函数的单调性求出值域D,然后由D[﹣3,1]可得关于m的不等式组,解出即可;
【考点精析】关于本题考查的函数单调性的判断方法和函数奇偶性的性质,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E. 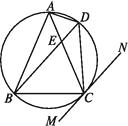
(1)求证:△ABE≌△ACD;
(2)求证:BE=BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间; 
(2)写出函数f(x)的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市五一假期举行促销活动,规定一次购物不超过100元的不给优惠;超过100元而不超过300元时,按该次购物全额9折优惠;超过300元的其中300 元仍按9折优惠,超过部分按8折优惠.
(1)写出顾客购物全额与应付金额之间的函数关系,并画出流程图,要求输入购物全额,能输出应付金额.
(2)若某顾客的应付金额为282.8元,请求出他的购物全额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,則第20行从左至右的第4个数字应是 . 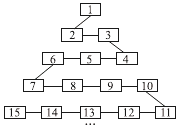
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】顶点在原点,焦点在x轴正半轴的抛物线,经过点(3,6),
(1)求抛物线截直线y=2x﹣6所得的弦长.
(2)讨论直线y=kx+1与抛物线的位置关系,并求出相应的k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣5x﹣6<0},集合B={x|6x2﹣5x+1≥0},集合 ![]()
(1)求A∩B;
(2)若A∪C=C,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com