
如图,已知抛物线 :
: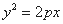 和⊙
和⊙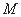 :
: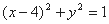 ,过抛物线
,过抛物线 上一点H作两条直线与⊙
上一点H作两条直线与⊙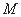 相切于
相切于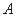 、
、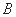 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点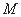 到抛物线准线的距离为
到抛物线准线的距离为 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)当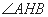 的角平分线垂直
的角平分线垂直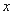 轴时,求直线
轴时,求直线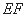 的斜率;
的斜率;

科目:高中数学 来源: 题型:
某大学的一个社会实践调查小组,在对大学生的良好“光盘习惯”的调査中,随机发放了l20份问巻。对收回的l00份有效问卷进行统计,得到如下2 x2列联表:
| 做不到光盘 | 能做到光盘 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
(1)现已按是否能做到光盘分层从45份女生问卷中抽取了9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为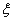 ,试求随机变量
,试求随机变量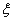 的分布列和数学期望
的分布列和数学期望
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P,那么根据临界值表最精确的P的值应为多少?请说明理由。
附:独立性检验统计量K2=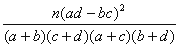 , 其中
, 其中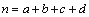 ,
,
独立性检验临界表:
| P(K2 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
若集合A={x∈R|x+1>0 },集合B={x∈R|(x-1)(x+2)<0 },则A∩B=
A.(-1,1) B.(-2,-1) C.(-∞,-2) D.(1,+∞),
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两点A(1,0)、B(1,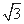 ),O 为坐标原点,点C 在第二象限,且∠AOC =120°,设
),O 为坐标原点,点C 在第二象限,且∠AOC =120°,设 = -2
= -2 ,则λ 等于( )
,则λ 等于( )
A.-1 B.2 C.1 D.-2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知F1、F2是椭圆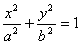 的左、右焦点,O为坐标原点,点
的左、右焦点,O为坐标原点,点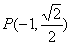 在椭圆上,线段PF2与y轴的交点M满足
在椭圆上,线段PF2与y轴的交点M满足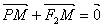 ;
;
(Ⅰ)求椭圆的标准方程;
(Ⅱ)⊙O是以F1F2为直径的圆,一直线l: y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.当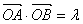 ,且满足
,且满足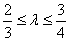 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com