
【题目】如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′﹣DEF的体积最大值为 ![]() a3;
a3;
④动点A′在平面ABC上的射影在线段AF上;
⑤二面角A′﹣DE﹣F大小的范围是[0, ![]() ].
].
其中正确的命题是(写出所有正确命题的编号)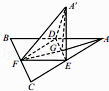
【答案】①②③④
【解析】解:①由已知可得四边形ADEF是菱形,则DE⊥GA′,DE⊥GF, ∴DE⊥平面A′FG,∴平面A′FG⊥平面ABC,①正确;
②由三角形中位线定理可得BC∥DE,∴BC∥平面A′DE,∴②正确;
③当面A′DE⊥面ABC时,三棱锥A′﹣DEF的体积达到最大,
最大值为 ![]() =
= ![]() ,③正确;
,③正确;
④由平面A′FG⊥平面ABC,可知点A′在面ABC上的射影在线段AF上,∴④正确;
⑤在旋转过程中二面角A′﹣DE﹣F大小的范围是[0,π],∴⑤不正确.
故答案为:①②③④.
①由已知可得四边形ADEF是菱形,再利用菱形对角线的性质、线面面面垂直的判定与性质定理即可得出;②由三角形中位线定理和线面平行的判定定理即可得出;③当面A′DE⊥面ABC时,三棱锥A′﹣DEF的体积达到最大,再利用体积计算公式即可得出;④由平面A′FG⊥平面ABC,利用面面垂直的性质定理可得点A′在面ABC上的射影在线段AF上;⑤在旋转过程中二面角A′﹣DE﹣F大小的范围是[0,π],即可判断出.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】设四棱锥P﹣ABCD的底面不是平行四边形,用平面 α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α( ) 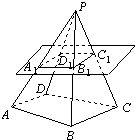
A.不存在
B.只有1个
C.恰有4个
D.有无数多个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的半径为1,圆心C(a,2a﹣4),(其中a>0),点O(0,0),A(0,3)
(1)若圆C关于直线x﹣y﹣3=0对称,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点P,使|PA|=|2PO|,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于实数x的不等式﹣x2+bx+c<0的解集是{x|x<﹣3或x>2},则关于x的不等式cx2﹣bx﹣1>0的解集是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣2,3)
C.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣2)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在平行四边形ABB1A1中,∠ABB1=60°,AB=4,AA1=2,C,C1分别为AB,A1B1的中点,现把平行四边形ABB1A1沿CC1折起如图2所示,连接B1C,B1A,B1A1 . 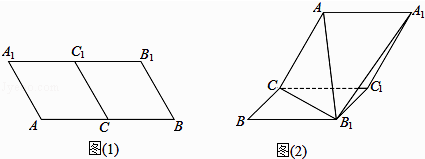
(1)求证:AB1⊥CC1;
(2)若AB1= ![]() ,求二面角C﹣AB1﹣A1的余弦值.
,求二面角C﹣AB1﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
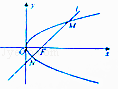
【题目】已知抛物线y2=2px(p>0)的焦点为F与椭圆C的一个焦点重合,且抛物线的准线与椭圆C相交于点 ![]() .
. 
(1)求抛物线的方程;
(2)过点F是否存在直线l与椭圆C交于M,N两点,且以MN为对角线的正方形的第三个顶点恰在y轴上?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+m.
(1)试用定义证明:函数f(x)在(0,+∞)上单调递增;
(2)若关于x的不等式f(x)≥x3+3x2﹣3x在区间[1,2]上有解,求m的取值范围.参考公式:a3﹣b3=(a﹣b)(a2+ab+b2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面为正方形且各侧棱长均相等的四棱锥V﹣ABCD可绕着棱AB任意旋转,若AB平面α,M,N分别是AB,CD的中点,AB=2,VA= ![]() ,点V在平面α上的射影为点O,则当ON的最大时,二面角C﹣AB﹣O的大小是( )
,点V在平面α上的射影为点O,则当ON的最大时,二面角C﹣AB﹣O的大小是( ) 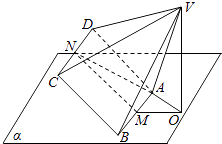
A.90°
B.105°
C.120°
D.135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com