
【题目】如图,底面为正方形且各侧棱长均相等的四棱锥V﹣ABCD可绕着棱AB任意旋转,若AB平面α,M,N分别是AB,CD的中点,AB=2,VA= ![]() ,点V在平面α上的射影为点O,则当ON的最大时,二面角C﹣AB﹣O的大小是( )
,点V在平面α上的射影为点O,则当ON的最大时,二面角C﹣AB﹣O的大小是( ) 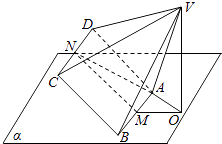
A.90°
B.105°
C.120°
D.135°
【答案】B
【解析】解:设∠VMO=θ,
则∵M、N分别是AB、CD的中点,AB=2,VA= ![]() ,
,
∴AM=1,VM= ![]() =
= ![]() =2,
=2,
MN=BC=AB=2,VN=VM=2,
则三角形VNM为正三角形,则∠NMV=60°,
则OM=2cosθ,
在三角形OMN中,
ON2=MN2+OM2﹣2MNOMcos(60°+θ)=4+4cos2θ﹣2×2×2cosθcos(60°+θ)
=4+4cos2θ﹣8cosθ( ![]() cosθ﹣
cosθ﹣ ![]() sinθ)
sinθ)
=4+4cos2θ﹣4cos2θ+4 ![]() sinθcosθ
sinθcosθ
=4+2 ![]() sin2θ,
sin2θ,
∴要使ON最大,则只需要sin2θ=1,即2θ=90°即可,则θ=45°,
此时二面角C﹣AB﹣O的大小∠OMN=60°+θ=60°+45°=105°,
故选:B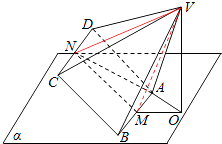


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′﹣DEF的体积最大值为 ![]() a3;
a3;
④动点A′在平面ABC上的射影在线段AF上;
⑤二面角A′﹣DE﹣F大小的范围是[0, ![]() ].
].
其中正确的命题是(写出所有正确命题的编号)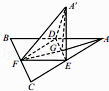
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】欧巴老师布置给时镇同学这样一份数学作业:在同一个直角坐标系中画出四个对数函数的图象,使它们的底数分别为 ![]() 和
和 ![]() .时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为e的对数函数图象?”时镇同学无言以对,憋得满脸通红,眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?曲线才是底数为e的对数函数的图象.
.时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为e的对数函数图象?”时镇同学无言以对,憋得满脸通红,眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?曲线才是底数为e的对数函数的图象.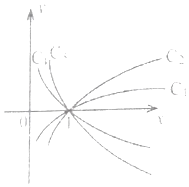
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知α∈(0, ![]() ),β∈(0,
),β∈(0, ![]() ),且满足
),且满足 ![]() cos2
cos2 ![]() +
+ ![]() sin2
sin2 ![]() =
= ![]() +
+ ![]() ,sin(2017π﹣α)=
,sin(2017π﹣α)= ![]() cos(
cos( ![]() π﹣β),则α+β= .
π﹣β),则α+β= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,记正方形ABCD四条边的中点为S,M,N,T,连接四个中点得小正方形SMNT.将正方形ABCD,正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1 , V2 , 则V1:V2=( ) 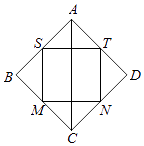
A.8:1
B.2:1
C.4:3
D.8:3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x﹣lnx(x>0),则函数f(x)( )
x﹣lnx(x>0),则函数f(x)( )
A.在区间(0,1)内有零点,在区间(1,+∞)内无零点
B.在区间(0,1)内有零点,在区间(1,+∞)内有零点
C.在区间(0,3),(3,+∞)均无零点
D.在区间(0,3),(3,+∞)均有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下面四个命题: (1.)从匀速传递的产品生产流水线上,质检员每15分钟从中抽取一件产品进行某项指标检测,这样的抽样是系统抽样;
(2.)两个随机变量相关性越强,则相关系数的绝对值越接近于1;
(3.)对分类变量X和Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大;
(4.)在回归直线方程 ![]() =0.4x+12中,当解释变量x每增加一个单位时,预报变量大约增加0.4个单位.
=0.4x+12中,当解释变量x每增加一个单位时,预报变量大约增加0.4个单位.
其中真命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com