
分析 定义域容易看出为(4,+∞),可将原函数变成$f(x)=\sqrt{x-4}+\frac{1}{\sqrt{x-4}}$,根据基本不等式即可得出f(x)≥2,即得出f(x)的值域.
解答 解:要使f(x)有意义,则x>4;
∴该函数定义域为(4,+∞);
$f(x)=\frac{x-4+1}{\sqrt{x-4}}=\sqrt{x-4}+\frac{1}{\sqrt{x-4}}$≥2,当$\sqrt{x-4}=\frac{1}{\sqrt{x-4}}$,即x=5时取“=”;
∴该函数的值域为[2,+∞).
故答案为:(4,+∞),[2,+∞).
点评 考查函数定义域、值域的概念及求法,基本不等式用于求函数值域,注意判断等号能否取到.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{8}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
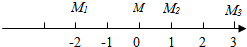 三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)
三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com