
 如图所示,矩形ABCD的对角线交于点G,AD⊥平面ABE,AE=2
如图所示,矩形ABCD的对角线交于点G,AD⊥平面ABE,AE=2| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| ||
| 3 |


科目:高中数学 来源: 题型:
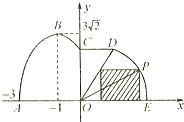 如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,| π |
| 2 |
| 2 |
| 3 |
 |
| DE |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省南京市金陵中学高考数学预测试卷(2)(解析版) 题型:解答题
 <φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3
<φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3 );赛道的中间部分为
);赛道的中间部分为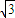 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分14分)
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y= (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com