
| A. | (-1,0)∪(1,+∞) | B. | (-∞,-1)∪(e,+∞) | C. | (-e,0)∪(e,+∞) | D. | (-∞,-e)∪(0,e) |
分析 先求出f(x)的解析式,问题转化为解不等式xln|x|>0,通过讨论x的范围,求出不等式的解集即可.
解答 解:∵x>0时,xf′(x)-f(x)=x,
∴$\frac{xf′(x)-f(x)}{{x}^{2}}$=$\frac{1}{x}$,
即${[\frac{f(x)}{x}]}^{′}$=$\frac{1}{x}$,
∴f(x)=x(lnx+c),
若f(e)=e,则e(lne+c)=e,解得:c=0,
∴f(x)=xlnx,(x>0),
∵f(x)是奇函数,
∴f(x)=xln|x|,
由f(x)>0,即xln|x|>0,
得:$\left\{\begin{array}{l}{x>0}\\{lnx>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{ln(-x)<0}\end{array}\right.$,
解得:x>1或-1<x<0,
故选:A.
点评 本题考查了导数的应用,考查求函数的原函数问题,考查不等式的解法,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -e | B. | -$\frac{e}{2}$ | C. | $\frac{e}{2}$ | D. | e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
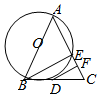 已知:AB为圆O的直径,AB=AC,AC,BC分别交圆O于E,D,连接BE,DF⊥AC于F
已知:AB为圆O的直径,AB=AC,AC,BC分别交圆O于E,D,连接BE,DF⊥AC于F查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
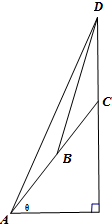 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD.为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进25m到达B处,又测得∠DBC=45°.根据以上数据计算可得cosθ=$\frac{\sqrt{3}-1}{2}$.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD.为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进25m到达B处,又测得∠DBC=45°.根据以上数据计算可得cosθ=$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com