
| A. | -e | B. | -$\frac{e}{2}$ | C. | $\frac{e}{2}$ | D. | e |
分析 先求出f(x)的表达式,求出f(x)的导数,得到函数的单调区间,从而求出函数的最小值即可.
解答 解:∵xf′(x)-f(x)=x2lnx,
∴$\frac{xf′(x)-f(x)}{{x}^{2}}$=lnx,
∴${[\frac{f(x)}{x}]}^{′}$=lnx,
∴$\frac{f(x)}{x}$=xlnx-x+c,
∵f(1)=-1,
∴f(1)=-1+c=-1,解得:c=0,
∴f(x)=x2(lnx-1),
∴f′(x)=x(2lnx-1),
令f′(x)>0,解得:x>$\sqrt{e}$,令f′(x)<0,解得:0<x<$\sqrt{e}$,
∴f(x)在(0,$\sqrt{e}$)递减,在($\sqrt{e}$,+∞)递增,
∴f(x)min=f($\sqrt{e}$)=-$\frac{e}{2}$,
故选:B.
点评 本题考查了函数的单调性问题,考查导数的应用以及求函数的原函数问题,是一道中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {x∈R|x≤1} | B. | {x∈R|x<1} | C. | {x∈R|0<x≤1} | D. | {x∈R|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,过点P作⊙O的切线PA,A为切点,割线PB交⊙O于点B、C,R为⊙O上的点,且有AC=AR.
如图所示,过点P作⊙O的切线PA,A为切点,割线PB交⊙O于点B、C,R为⊙O上的点,且有AC=AR.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(1,+∞) | B. | (-∞,-1)∪(e,+∞) | C. | (-e,0)∪(e,+∞) | D. | (-∞,-e)∪(0,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0∈(0,1) | B. | x0∈(1,2) | C. | x0∈(2,3) | D. | x0∈(3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
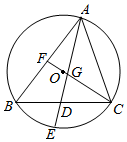 如图,⊙O是△ABC的外接圆,∠BAC的平分线AD交BC于D,交⊙O于E,连接CO并延长,交AE于G,交AB于F.
如图,⊙O是△ABC的外接圆,∠BAC的平分线AD交BC于D,交⊙O于E,连接CO并延长,交AE于G,交AB于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com