
分析 画出函数y=|f(x)|的图象,由题意得出a的取值范围和x1x2,x3+x4的值,再利用基本不等式即可求出ax1x2+$\frac{{{x_3}+{x_4}}}{a}$的取值范围.
解答 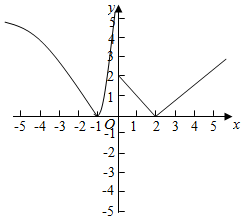 解:由题意,画出函数y=|f(x)|的图象,如图所示,
解:由题意,画出函数y=|f(x)|的图象,如图所示,
又函数g(x)=a-|f(x)|有四个零点x1,x2,x3,x4,且x1<x2<x3<x4,
所以0<a≤2,
且log2(-x1)=-log2(-x2)=2-x3=x4-2,
所以x1x2=1,x3+x4=4,
所以ax1x2=a,
$\frac{{x}_{3}{+x}_{4}}{a}$=$\frac{4}{a}$,
所以ax1x2+$\frac{{{x_3}+{x_4}}}{a}$=a+$\frac{4}{a}$≥2$\sqrt{a•\frac{4}{a}}$=4,当且仅当a=2时“=”成立;
所以ax1x2+$\frac{{{x_3}+{x_4}}}{a}$的取值范围是[4,+∞).
故答案为:[4,+∞).
点评 本题考查了分段函数研究函数的零点的应用问题,也考查了取值范围的确定与等价转化的应用问题,是综合性题目.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
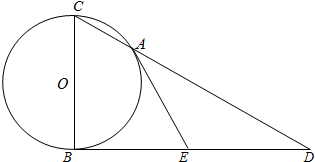 如图,过⊙O外一点E作⊙O的两条切线EA、EB,其中A、B为切点,BC为⊙O的一条直径,连CA并延长交BE的延长线于D点.
如图,过⊙O外一点E作⊙O的两条切线EA、EB,其中A、B为切点,BC为⊙O的一条直径,连CA并延长交BE的延长线于D点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -e | B. | -$\frac{e}{2}$ | C. | $\frac{e}{2}$ | D. | e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
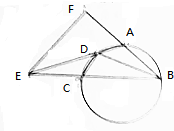 如图,A、B、C、D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A、B、C、D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
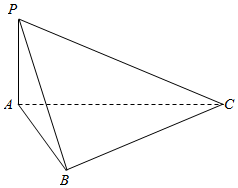 如图,在三棱锥P-ABC中,已知PA⊥平面ABC,平面PAB⊥平面PBC
如图,在三棱锥P-ABC中,已知PA⊥平面ABC,平面PAB⊥平面PBC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x<3x | B. | $\frac{1}{{{x^2}-x+1}}$>$\frac{1}{{{x^2}+x+1}}$ | ||
| C. | $\frac{1}{{{x^2}+1}}$>$\frac{1}{{{x^2}+2}}$ | D. | 2|x|<x2+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com