
分析 已知等式利用正弦定理化简,再利用两角和与差的正弦函数公式及诱导公式变形,求出tanB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;
解答 解:因为a=bcosC+csinB,由正弦定理知sinA=sinBcosC+sinCsinB①,
在△ABC中,A=π-(B+C)②,
由①和②得sinBsinC=cosBsinC,
而C∈(0,π),
所以sinC≠0,
所以sinB=cosB,
又B∈(0,π),
所以B=$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 此题考查了正弦定理,两角和与差的正弦函数公式,熟练掌握定理及公式是解本题的关键,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
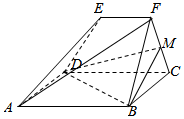 如图,已知多面体ABCDEF中,ABCD为正方形,EF∥平面ABCD,M为FC的中点,AB=2,EF到平面ABCD的距离为2.
如图,已知多面体ABCDEF中,ABCD为正方形,EF∥平面ABCD,M为FC的中点,AB=2,EF到平面ABCD的距离为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{2}$ | B. | $\frac{49}{2}$ | C. | 12 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x∈R|x≤1} | B. | {x∈R|x<1} | C. | {x∈R|0<x≤1} | D. | {x∈R|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
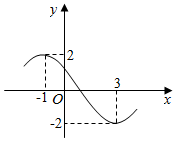
| A. | 0 | B. | 1 | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(1,+∞) | B. | (-∞,-1)∪(e,+∞) | C. | (-e,0)∪(e,+∞) | D. | (-∞,-e)∪(0,e) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com