Question

18．已知?x∈（0，+∞），[（m-1）x-1]（x²-mx-1）≥0恒成立，则m的值为$\frac{3}{2}$．

Answer 1

分析 对m≤1和m＞1分类，若m≤1，由x＞0，可得（m-1）x-1＜0，而y=x²-mx-1的图象开口向上，可知[（m-1）x-1]（x²-mx-1）≥0不恒成立，因此m＞1，由（m-1）x-1=0，解得x=$\frac{1}{m-1}$＞0，而方程x²-mx-1=0的两个实数根异号，x=$\frac{1}{m-1}$必定是方程x²-mx-1=0的一个正根，把x=$\frac{1}{m-1}$代入方程x²-mx-1=0，求解可得m的值．

解答 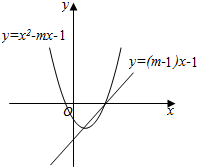解：若m≤1，∵x＞0，∴（m-1）x-1＜0，
又y=x²-mx-1的图象开口向上，
∴[（m-1）x-1]（x²-mx-1）≥0不恒成立，
因此m＞1，如图：
由（m-1）x-1=0，解得x=$\frac{1}{m-1}$＞0，而方程x²-mx-1的两个实数根异号，
要使?x∈（0，+∞），[（m-1）x-1]（x²-mx-1）≥0恒成立，
∴x=$\frac{1}{m-1}$必定是方程x²-mx-1的一个正根，
把x=$\frac{1}{m-1}$代入方程x²-mx-1可得：$（\frac{1}{m-1}）^{2}-\frac{m}{m-1}-1=0$，
又m＞1，解得m=$\frac{3}{2}$．
故答案为：$\frac{3}{2}$．

点评 本题考查恒成立问题，考查了二次函数的单调性、一元二次方程的解与函数的零点，关键是掌握等价转化方法，考查了推理能力和计算能力，将条件转化为方程（m-1）x-1=0与x²-mx-1=0在（0，+∞）上有相同零点是解决本题的关键，综合性强，难度较大．