解:函数
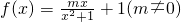
的定义域为R,
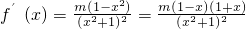
.
①当m>0时,当x变化时,f
′(x),f(x)的变化情况如表:

所以,函数f(x)的单调增区间时(-1,1),单调递减区间是(-∞,-1),(1,+∞).
②当m<0时,当x变化时,f
′(x),f(x)的变化情况如表:
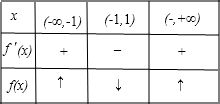
所以,函数f(x)的单调减区间时(-1,1),单调递增区间是(-∞,-1),(1,+∞).
(Ⅱ)依题意,对任意当m>0时,对于任意x
1,x
2∈[0,2],f(x
1)≥g(x
2)恒成立,等价于
当m>0时,对于任意x
1,x
2∈[0,2],f(x)
min≥g(x)
max成立.
当m>0时,由(Ⅰ)知,函数f(x)在[0,1]上单调递增,在[1,2]上单调递减,
因为f(0)=1,f(2)=
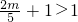
,所以函数f(x)的最小值为f(0)=1.
所以应满足g(x)
max≤1.
因为g(x)=x
2e
ax,所以g
′(x)=(ax
2+2x)e
ax.
③当a=0时,函数g(x)=x
2,任意x∈[0,2],g(x)
max=g(2)=4,
显然不满足g(x)
max≤1,故a=0不成立.
④当a≠0时,令g
′(x)=(ax
2+2x)e
ax=0得:
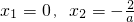
1°当
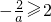
,即-1≤a<0时,在[0,2]上g
′(x)≥0,所以函数g(x)在[0,2]上单调递增,
所以
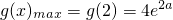
.
由4e
2a≤1得,a≤-ln2,所以-1≤a≤-ln2.
2°当0<
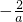
<2,即a<-1时,在
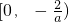
上g
′(x)≥0,在
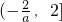
上g
′(x)<0,
所以函数g(x)在
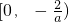
上单调递增,在
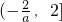
上单调递减.
所以
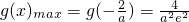
.
由
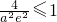
得:
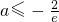
,所以a<-1.
3°当
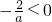
,即a>0时,显然在[0,2]上g
′(x)≥0,
函数g(x)在[0,2]上单调递增,且
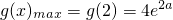
.
显然
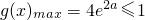
不成立,故a>0不成立.
综上所述,a的取值范围是(-∞,-ln2].
分析:(Ⅰ)把给出的函数进行求导,由导函数的零点把定义域分段,然后分m的正负判断导函数在各区间段内的符号,从而得到元函数的单调区间;
(Ⅱ)当m>0时,若对任意x
1,x
2∈[0,2],f(x
1)≥g(x
2)恒成立,转化为对于任意x
1,x
2∈[0,2],f(x)
min≥g(x)
max成立,然后分类求函数f(x)和g(x)在[0,2]上的最小值和最大值,由f(x)的最小值大于g(x)的最大值即可解得实数a的取值范围.
点评:本题考查了利用导数研究函数的单调性,考查了函数恒成立问题,解答过程体现了分类讨论得数学思想,正确对a进行分类是解答该题的关键,此题属有一定难度题目.

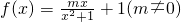 ,g(x)=x2eax(a∈R).
,g(x)=x2eax(a∈R).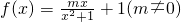 的定义域为R,
的定义域为R,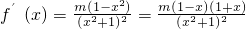 .
.

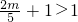 ,所以函数f(x)的最小值为f(0)=1.
,所以函数f(x)的最小值为f(0)=1.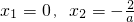
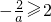 ,即-1≤a<0时,在[0,2]上g′(x)≥0,所以函数g(x)在[0,2]上单调递增,
,即-1≤a<0时,在[0,2]上g′(x)≥0,所以函数g(x)在[0,2]上单调递增,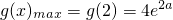 .
.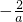 <2,即a<-1时,在
<2,即a<-1时,在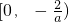 上g′(x)≥0,在
上g′(x)≥0,在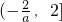 上g′(x)<0,
上g′(x)<0,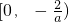 上单调递增,在
上单调递增,在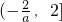 上单调递减.
上单调递减.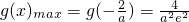 .
.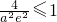 得:
得: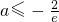 ,所以a<-1.
,所以a<-1.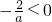 ,即a>0时,显然在[0,2]上g′(x)≥0,
,即a>0时,显然在[0,2]上g′(x)≥0,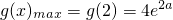 .
.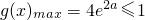 不成立,故a>0不成立.
不成立,故a>0不成立.
