
【题目】如图1是淋浴房示意图,它的底座是由正方形截去一角得到,这一角是一个与正方形两邻边相切的圆的![]() 圆弧(如图2).现已知正方形的边长是1米,设该底座的面积为S平方米,周长为l米(周长是指图2中实线部分),圆的半径为r米.设计的理想要求是面积S尽可能大,周长l尽可能小,但显然S、l都是关于r的减函数,于是设
圆弧(如图2).现已知正方形的边长是1米,设该底座的面积为S平方米,周长为l米(周长是指图2中实线部分),圆的半径为r米.设计的理想要求是面积S尽可能大,周长l尽可能小,但显然S、l都是关于r的减函数,于是设![]() ,当
,当![]() 的值越大,满意度就越高.试问r为何值时,该淋浴房底座的满意度最高?(解答时π以3代入运算)
的值越大,满意度就越高.试问r为何值时,该淋浴房底座的满意度最高?(解答时π以3代入运算)

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() 是由两个全等的菱形
是由两个全等的菱形![]() 和
和![]() 组成的空间图形,
组成的空间图形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
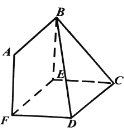
(1)求证:![]() ;
;
(2)如果二面角B-EF-D的平面角为60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省开展“精准脱贫,携手同行”的主题活动,某贫困县统计了100名基层干部走访贫困户的数量,并将走访数量分成5组,统计结果见下表.
走访数量区间 | 频数 | 频率 |
| b | |
| 10 | |
| 38 | |
| a | 0.27 |
| 9 | |
总计 | 100 | 1.00 |
(1)求a与b的值;
(2)根据表中数据,估计这100名基层干部走访数量的中位数(精确到个位);
(3)如果把走访贫困户不少于35户视为“工作出色”,按照分层抽样,从“工作出色”的基层干部中抽取4人,再从这4人中随机抽取2人,求其中有1人走访贫困户不少于45户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案(a)规定每日底薪50元,快递业务每完成一单提成3元;方案(b)规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元,该快餐连锁店记录了每天骑手的人均业务量,现随机抽取100天的数据,将样本数据分为[ 25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图.

(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)从以往统计数据看,新聘骑手选择日工资方案(a)的概率为![]() ,选择方案(b)的概率为
,选择方案(b)的概率为![]() .若甲、乙、丙三名骑手分别到该快餐连锁店应聘,三人选择日工资方案相互独立,求至少有两名骑手选择方案(a)的概率;
.若甲、乙、丙三名骑手分别到该快餐连锁店应聘,三人选择日工资方案相互独立,求至少有两名骑手选择方案(a)的概率;
(3)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ={1,2,3,…,n}(其中n≥3,n
={1,2,3,…,n}(其中n≥3,n![]() ),将
),将![]() 的所有3元子集(含有3个元素的子集)中的最小元素的和记为
的所有3元子集(含有3个元素的子集)中的最小元素的和记为![]() .
.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)试求![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为1,
的面积为1,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 、
、![]() 是椭圆的左右两个焦点,直线
是椭圆的左右两个焦点,直线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 点的横坐标;若不存在,请说明理由.
点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上具有单调性,求
上具有单调性,求![]() 的取值范围;
的取值范围;
(3)若函数![]()
![]() 有且仅有
有且仅有![]() 个不同的零点
个不同的零点![]() ,且
,且![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com