
【题目】设函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上具有单调性,求
上具有单调性,求![]() 的取值范围;
的取值范围;
(3)若函数![]()
![]() 有且仅有
有且仅有![]() 个不同的零点
个不同的零点![]() ,且
,且![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)根据![]() ,对函数求导,求出
,对函数求导,求出![]() ,
,![]() ,进而可得切线方程;
,进而可得切线方程;
(2)先对函数求导,得到![]() ,分别讨论函数
,分别讨论函数![]() 在区间
在区间![]() 上单调递增,函数
上单调递增,函数![]() 在区间
在区间![]() 上单调递减,两种情况,即可求出参数范围;
上单调递减,两种情况,即可求出参数范围;
(3)先由题意,得到![]() 有且仅有两个不等于
有且仅有两个不等于![]() 的不同零点,设
的不同零点,设![]() ,对函数求导,得出
,对函数求导,得出![]() 的单调性,推出
的单调性,推出![]() 有且仅有两个不等实数根,且一个根小于
有且仅有两个不等实数根,且一个根小于![]() ,一个根大于
,一个根大于![]() ,再由题意,得到
,再由题意,得到![]() ,
,![]() 为
为![]() 的两个不等实数根,推出
的两个不等实数根,推出![]() ,设
,设![]() ,
,![]() ,
,![]() ,对其求导,研究其单调性,进而可得出结果.
,对其求导,研究其单调性,进而可得出结果.
解:(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(2)因为![]() ,
,
①若函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() 恒成立,得
恒成立,得![]() 恒成立,
恒成立,
∵![]() ,∴
,∴![]() ,所以
,所以![]() ;
;
②若函数![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() 恒成立,得
恒成立,得![]() 恒成立,
恒成立,
∵![]() ,∴
,∴![]() ,所以
,所以![]() ;
;
综上,![]() 的取值范围为
的取值范围为![]() .
.
(3)函数![]()
![]() 的零点即为方程
的零点即为方程![]() 的实数根,
的实数根,
故![]() 或
或![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() 有且仅有两个不等于
有且仅有两个不等于![]() 的不同零点,
的不同零点,
由![]() ,得
,得![]() ,设
,设![]() ,
,
则![]() ,由
,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() 有且仅有两个不等实数根,且一个根小于
有且仅有两个不等实数根,且一个根小于![]() ,一个根大于
,一个根大于![]() ,
,
∵![]() 有且仅有
有且仅有![]() 个不同的零点
个不同的零点![]() ,
,![]() ,
,
∴![]() ,
,![]() 为
为![]() 的两个不等实数根,
的两个不等实数根,
∴![]() ,
,![]() ,两式相减,得
,两式相减,得![]() ,∴
,∴![]() ,
,
两式相加,得![]() ,
,
设![]() ,由
,由![]() 且
且![]() ,得
,得![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
则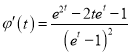 ,设
,设![]() ,
,![]() ,则
,则![]() ,
,
设![]() ,
,![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 在
在![]() 上恒成立,
上恒成立,
则![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,,
,,![]() ,即
,即![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】如图1是淋浴房示意图,它的底座是由正方形截去一角得到,这一角是一个与正方形两邻边相切的圆的![]() 圆弧(如图2).现已知正方形的边长是1米,设该底座的面积为S平方米,周长为l米(周长是指图2中实线部分),圆的半径为r米.设计的理想要求是面积S尽可能大,周长l尽可能小,但显然S、l都是关于r的减函数,于是设
圆弧(如图2).现已知正方形的边长是1米,设该底座的面积为S平方米,周长为l米(周长是指图2中实线部分),圆的半径为r米.设计的理想要求是面积S尽可能大,周长l尽可能小,但显然S、l都是关于r的减函数,于是设![]() ,当
,当![]() 的值越大,满意度就越高.试问r为何值时,该淋浴房底座的满意度最高?(解答时π以3代入运算)
的值越大,满意度就越高.试问r为何值时,该淋浴房底座的满意度最高?(解答时π以3代入运算)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】作家马伯庸小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行,每一列上至多有一个紫色小方格(如图所示即满足要求).则一共可以传递______种信息.(用数字作答)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为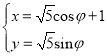 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)求C1的极坐标方程;
(2)若C1与曲线C2:ρ=2sinθ交于A,B两点,求|OA||OB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】火箭少女101的新曲《卡路里》受到了广大听众的追捧,歌词积极向上的体现了人们对于健康以及完美身材的渴望.据有关数据显示,成年男子的体脂率在14%-25%之间.几年前小王重度肥胖,在专业健身训练后,身材不仅恢复正常,且走上美体路线.通过整理得到如下数据及散点图.
健身年数 | 1 | 2 | 3 | 4 | 5 | 6 |
体脂率 | 32 | 20 | 12 | 8 | 6.4 | 4.4 |
| 3.4 | 3 | 2.5 | 2.1 | 1.9 | 1.5 |
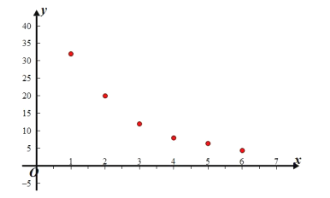
(1)根据散点图判断,![]() 与
与![]() 哪一个模型更适宜作为体脂率关于健身年数的回归方程模型(给出选择即可)
哪一个模型更适宜作为体脂率关于健身年数的回归方程模型(给出选择即可)
(2)根据(1)的判断结果与题目中所给数据,建立![]() 与
与![]() 的回归方程.(保留一位小数)
的回归方程.(保留一位小数)
(3)再坚持3年,体脂率可达到多少.
参考公式: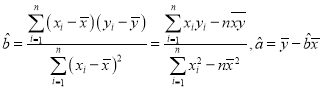
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三梭柱ABC-A1B1C1中,AC=BC,E,F分别为AB,A1B1的中点.
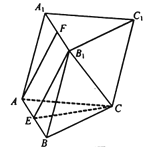
(1)求证:AF∥平面B1CE;
(2)若A1B1⊥![]() ,求证:平面B1CE⊥平面ABC.
,求证:平面B1CE⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望;
(II) 取出的3件产品中一等品件数多于二等品件数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌电脑体验店预计全年购入![]() 台电脑,已知该品牌电脑的进价为
台电脑,已知该品牌电脑的进价为![]() 元/台,为节约资金决定分批购入,若每批都购入
元/台,为节约资金决定分批购入,若每批都购入![]() (
(![]() 为正整数)台,且每批需付运费
为正整数)台,且每批需付运费![]() 元,储存购入的电脑全年所付保管费与每批购入电脑的总价值(不含运费)成正比(比例系数为
元,储存购入的电脑全年所付保管费与每批购入电脑的总价值(不含运费)成正比(比例系数为![]() ),若每批购入
),若每批购入![]() 台,则全年需付运费和保管费
台,则全年需付运费和保管费![]() 元.
元.
(1)记全年所付运费和保管费之和为![]() 元,求
元,求![]() 关于
关于![]() 的函数.
的函数.
(2)若要使全年用于支付运费和保管费的资金最少,则每批应购入电脑多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com