练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆：的离心率为，焦距为.

    （1）求的方程；

    （2）若斜率为的直线与椭圆交于，两点（点，均在第一象限），为坐标原点.

    ①证明：直线的斜率依次成等比数列.

    ②若与关于轴对称，证明：.

    【答案】（1）； （2）①见解析；②见解析.

    【解析】

    （1）根据离心率、焦距和可解出，从而得到椭圆方程；（2）①设直线的方程为：，，，将直线方程与椭圆方程联立可得韦达定理的形式，从而求得；整理可知：，从而证得结论；②与关于轴对称可知，由①知，则，利用两角和差正切公式展开整理，根据基本不等式求得最小值，经验证等号无法取得，从而证得结论.

    （1）由题意可得：，解得：

    椭圆的方程为：

    （2）证明：①设直线的方程为：，，

    由消去得：

    则，且，

    即直线的斜率依次成等比数列

    ②由题可知：

    由①可知：，，

    若，则两点重合，不符合题意；可知无法取得等号

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某快餐连锁店招聘外卖骑手，该快餐连锁店提供了两种日工资方案：方案(a)规定每日底薪50元，快递业务每完成一单提成3元；方案(b)规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元，该快餐连锁店记录了每天骑手的人均业务量，现随机抽取100天的数据，将样本数据分为[ 25，35），[35，45)，[45，55)，[55，65)，[65，75)，[75，85)，[85，95]七组，整理得到如图所示的频率分布直方图.

    （1）随机选取一天，估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率；

    （2）从以往统计数据看，新聘骑手选择日工资方案（a）的概率为，选择方案（b）的概率为．若甲、乙、丙三名骑手分别到该快餐连锁店应聘，三人选择日工资方案相互独立，求至少有两名骑手选择方案(a)的概率；

    （3）若仅从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由．（同组中的每个数据用该组区间的中点值代替）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为，，上顶点为A，过的直线与y轴交于点M，满足（O为坐标原点），且直线l与直线之间的距离为.

    （1）求椭圆C的方程；

    （2）在直线上是否存在点P，满足？存在，指出有几个这样的点（不必求出点的坐标）；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二面角P﹣AB﹣C的大小为120°，且∠PAB＝∠ABC＝90°，AB＝AP，AB+BC＝6．若点P，A，B，C都在同一个球面上，则该球的表面积的最小值为（ ）

    A.45πB.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线与椭圆交于不同的两点，.

    （1）若线段的中点为，求直线的方程；

    （2）若的斜率为，且过椭圆的左焦点，的垂直平分线与轴交于点，求证：为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数（为自然对数的底数，）.

    （1）当时，求函数的图象在处的切线方程；

    （2）若函数在区间上具有单调性，求的取值范围；

    （3）若函数有且仅有个不同的零点，且，，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线，直线过焦点且与抛物线交于、两点，当直线的倾斜角为30°时，．

    （1）求抛物线方程．

    （2）在平面直角坐标系中，是否存在定点，当直线绕旋转时始终都满足平分．若存在，求出的坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用，从孩子一周岁生日开始，每年到银行储蓄元一年定期，若年利率为保持不变，且每年到期时存款（含利息）自动转为新的一年定期，当孩子18岁生日时不再存入，将所有存款（含利息）全部取回，则取回的钱的总数为　　

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动，治疗特种病的创新药研发成了当务之急．为此，某药企加大了研发投入，市场上治疗一类慢性病的特效药品的研发费用（百万元）和销量（万盒）的统计数据如下：

    研发费用（百万元）

    2

    3

    6

    10

    13

    15

    18

    21

    销量（万盒）

    1

    1

    2

    2.5

    3.5

    3.5

    4.5

    6

    （1）求与的相关系数精确到0.01，并判断与的关系是否可用线性回归方程模型拟合？（规定：时，可用线性回归方程模型拟合）；

    （2）该药企准备生产药品的三类不同的剂型，，，并对其进行两次检测，当第一次检测合格后，才能进行第二次检测．第一次检测时，三类剂型，，合格的概率分别为，，，第二次检测时，三类剂型，，合格的概率分别为，，．两次检测过程相互独立，设经过两次检测后，，三类剂型合格的种类数为，求的数学期望．

    附：（1）相关系数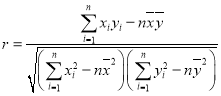

    （2），，，．

    查看答案和解析>>

    同步练习册答案