

图
(1)当∠QPA=60°时,请你对△QCP的形状作出猜想,并证明;
(2)当QP⊥AO时,△QCP的形状是___________三角形.
(3)由(1)、(2)得出的结论,请你进一步猜想,当点P在线段AM上运动到任何位置时△QCP一定是___________三角形.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 卡片号码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 取到的次数 | 13 | 8 | 5 | 7 | 6 | 13 | 18 | 10 | 11 | 9 |
| A、0.53 | B、0.5 |
| C、0.47 | D、0.37 |
查看答案和解析>>
科目:高中数学 来源: 题型:
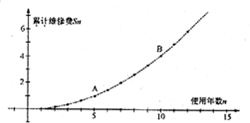 现在“汽车”是很“给力”的名词.汽车厂商对某款汽车的维修费进行电脑模拟试验,分别以汽车使用年限n和前n年累计维修费Sn(万元)为横、纵坐标绘制成点,发现点(n,Sn)在函数y=ax2+bx(a≠0)的图象上(如图所示),其中A(5,1.05)、B(10,4.1).
现在“汽车”是很“给力”的名词.汽车厂商对某款汽车的维修费进行电脑模拟试验,分别以汽车使用年限n和前n年累计维修费Sn(万元)为横、纵坐标绘制成点,发现点(n,Sn)在函数y=ax2+bx(a≠0)的图象上(如图所示),其中A(5,1.05)、B(10,4.1).| 车价+车主承担的维修费 | 使用年数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
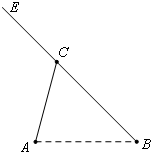 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.| 2 |
| 3 |
| 6 |
| 331 |
查看答案和解析>>
科目:高中数学 来源: 题型:
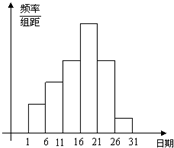 某市教育局在中学开展“创新素质实践行”小论文的评比.各校交论文的时间为5月1日至30日,评委会把各校交的论文的件数按5天一组分组统计,绘制了频率分布直方图(如图).已知从左至右各长方形的高的比为2:3:4:6:4:1,第二组的频数为18.那么本次活动收到论文的篇数是( )
某市教育局在中学开展“创新素质实践行”小论文的评比.各校交论文的时间为5月1日至30日,评委会把各校交的论文的件数按5天一组分组统计,绘制了频率分布直方图(如图).已知从左至右各长方形的高的比为2:3:4:6:4:1,第二组的频数为18.那么本次活动收到论文的篇数是( )查看答案和解析>>
科目:高中数学 来源: 题型:
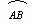
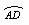
(1) (2)
图2-4-18
(1)求证:AB·DA=CD·BE;
(2)如图2-4-18(2),若点E在CB延长线上运动,使切线EA变为割线EFA,其他条件不变,问具备什么条件使原结论成立?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com