
 ���и���ѧҵˮƽ�����У�ijУ��ʦΪ���˽�����������100��ѧ������ѧ�÷���������ɼ��ֳ����飺[80��90����[90��100����[100��110����[110��120����[120��130����[130��140��ͳ���������£�
���и���ѧҵˮƽ�����У�ijУ��ʦΪ���˽�����������100��ѧ������ѧ�÷���������ɼ��ֳ����飺[80��90����[90��100����[100��110����[110��120����[120��130����[130��140��ͳ���������£�| ������ | [80��90�� | [90��100�� | [100��110�� | [110��120�� | [120��130�� | [130��140�� |
| ���� | 2 | 8 | 30 | 30 | 20 | 10 |
���� ������ͳ������������Ƶ�ʷֲ�ֱ��ͼ������Ƶ�ʷֲ�ֱ��ͼ�ܹ�����100ѧ������ѧƽ���ɼ���
���������⣬��[110��120����[120��130����[130��140�������У����÷ֲ������ȡ��ѧ�����ֱ�Ϊ3��2��1���εĿ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к�E�Σ�
��� �⣺������ͳ����������Ƶ�ʷֲ�ֱ��ͼ���£�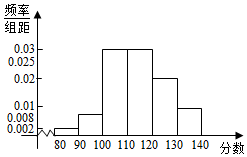
�������100ѧ������ѧƽ���ɼ���
$\overline{x}$=10��85��0.002+95��0.008+105��0.03+115��0.03125��0.02+135��0.01��=113.8��
���������⣬��[110��120����[120��130����[130��140�������У����÷ֲ������ȡ��ѧ�����ֱ�Ϊ3��2��1��
��εĿ���ȡֵΪ0��1��2��
P����=0��=$\frac{{C}_{2}^{0}{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{2}{5}$��
P����=1��=$\frac{{C}_{2}^{1}{C}_{4}^{1}}{{C}_{6}^{2}}$=$\frac{8}{15}$��
P����=2��=$\frac{{C}_{2}^{2}{C}_{4}^{0}}{{C}_{6}^{2}}$=$\frac{1}{15}$��
��εķֲ���Ϊ��
| �� | 0 | 1 | 2 |
| P | $\frac{2}{5}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��м����ʵ������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=$\frac{��}{12}$ | B�� | x=$\frac{5��}{12}$ | C�� | x=$\frac{��}{6}$ | D�� | x=$\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
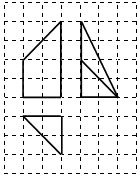 ��ͼ����ֽ��С�����εı߳�Ϊl����ʵ��ɽ����ij�����������ͼ�����������������Ϊ��������
��ͼ����ֽ��С�����εı߳�Ϊl����ʵ��ɽ����ij�����������ͼ�����������������Ϊ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
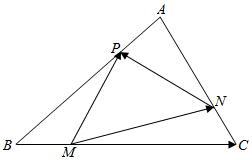 ��ͼ��M��N��P�ֱ���������ABC����BC��CA��AB�ϵĵ㣬������$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$����$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AC}$=$\overrightarrow{b}$��
��ͼ��M��N��P�ֱ���������ABC����BC��CA��AB�ϵĵ㣬������$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$����$\overrightarrow{AB}$=$\overrightarrow{a}$��$\overrightarrow{AC}$=$\overrightarrow{b}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 10 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | 2 | D�� | $2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\sqrt{2}-1$��1�� | B�� | [$\sqrt{2}$-1��1�� | C�� | ��2-$\sqrt{2}$��1�� | D�� | [2-$\sqrt{2}$��1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com