
| A. | ($\sqrt{2}-1$,1) | B. | [$\sqrt{2}$-1,1) | C. | (2-$\sqrt{2}$,1) | D. | [2-$\sqrt{2}$,1) |
分析 把已知等式变形,由椭圆的定义可得e(${x}_{0}+\frac{{a}^{2}}{c}$)=e•e($\frac{{a}^{2}}{c}-{x}_{0}$),解得P的横坐标x0,由题意可得-a≤x0≤a,再转化为关于e的不等式求得离心率e的取值范围.
解答 解:设点P的横坐标为x0,
由$\frac{a}{|P{F}_{2}|}$=$\frac{c}{|P{F}_{1}|}$,得|PF1|=e|PF2|,
则由椭圆的定义可得:e(${x}_{0}+\frac{{a}^{2}}{c}$)=e•e($\frac{{a}^{2}}{c}-{x}_{0}$),
解得:${x}_{0}=\frac{c-a}{e(e+1)}$,
∵P是椭圆上的点,∴-a≤$\frac{c-a}{e(e+1)}$≤a,
即-1≤$\frac{e-1}{e(e+1)}$≤1,
∴$\left\{\begin{array}{l}{e-1≥-{e}^{2}-e}\\{e-1≤{e}^{2}+e}\end{array}\right.$,即$\sqrt{2}-1≤e<1$,
则该椭圆的离心率e的取值范围是[$\sqrt{2}-1$,1),
故选:B.
点评 本题考查椭圆的第二定义,考查椭圆的简单性质的应用,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
 在市高三学业水平测试中,某校老师为了了解所教两个班100名学生的数学得分情况,按成绩分成六组:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)统计数据如下:
在市高三学业水平测试中,某校老师为了了解所教两个班100名学生的数学得分情况,按成绩分成六组:[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)统计数据如下:| 分数段 | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) |
| 人数 | 2 | 8 | 30 | 30 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
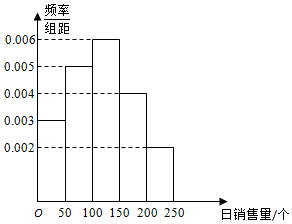 如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图.若一个月以30天计算,估计这家面包店一个月内日销售量不少于150个的天数为9.
如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图.若一个月以30天计算,估计这家面包店一个月内日销售量不少于150个的天数为9.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com