练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知动圆M与直线相切，且与定圆C：外切，

    求动圆圆心M的轨迹方程．

    求动圆圆心M的轨迹上的点到直线的最短距离．

    【答案】（1）； （2）.

    【解析】

    （1）设动圆圆心为M（x，y），半径为r，题目动点M（x，y）到C（0，﹣3）的距离等于点M到直线y＝3的距离，判断轨迹是抛物线方程，求解即可；

    （2）设直线方程为y＝x+m，，利用判别式为0，求出切线方程，利用平行线之间的距离求解即可．

    设动圆圆心为，半径为r，

    由题意知动点到的距离等于点M到直线的距离，

    由抛物线的定义可知，动圆圆心M的轨迹是以为焦点，以为准线的一条抛物线，

    故所求动圆圆心M的轨迹方程为：.

    （2）设直线方程为y＝x+m，，

    可得x2+12x+12m＝0，由△＝122﹣4×12m＝0，

    解得m＝3，d．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人是饮食以蔬菜为主；饮食指数高于70的人是饮食以肉类为主.

    (1)完成下列2×2列联表：

    能否有99％的把握认为老师的饮食习惯与年龄有关？

    (2)从群力校区任选一名老师, 设“选到45岁以上老师”为事件, “饮食指数高于70的老师”为事件, 用调查的结果估计及（用最简分数作答）；

    (3)为了给食堂提供老师的饮食信息, 根据(1)(2)的结论，能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.附:

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

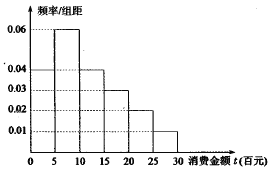
    【题目】“双十一”已经成为网民们的网购狂欢节，某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查，用随机抽样的方法抽取了100人，其消费金额 (百元)的频率分布直方图如图所示：

    (1)求网民消费金额的中位数；

    (2)把下表中空格里的数填上，能否有的把握认为网购消费与性别有关；

    (3)将(2)中的频率当作概率，电子商务平台从该市网民中随机抽取10人赠送电子礼金，求这10人中女性的人数的数学期望.

    男

    女

    合计

    30

    合计

    45

    附表：

    .

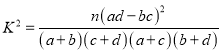    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为实常数，函数.

    （1）求函数的最值；

    （2）设.

    (i)讨论函数的单调性；

    （ⅱ） 若函数有两个不同的零点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， .

    （1）当时，求的单调区间；

    （2）当时，若对任意，都有成立，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，动点P从单位正方形ABCD顶点A开始，顺次经B、C、D绕边界一周，当 表示点P的行程， 表示PA之长时，求y关于x的解析式，并求 的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.表为10名学生的预赛成绩，其中有三个数据模糊.

    在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则（ ）

    A. 2号学生进入30秒跳绳决赛 B. 5号学生进入30秒跳绳决赛

    C. 8号学生进入30秒跳绳决赛 D. 9号学生进入30秒跳绳决赛

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动圆M与直线相切，且与定圆C：外切，

    求动圆圆心M的轨迹方程．

    求动圆圆心M的轨迹上的点到直线的最短距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为F，且过点A (2，2)，椭圆的离心率为，点B为抛物线C与椭圆D的一个公共点，且.

    (Ⅰ)求椭圆D的方程；

    (Ⅱ)过椭圆内一点P(0，t)的直线l的斜率为k，且与椭圆C交于M，N两点，设直线OM，ON(O为坐标原点)的斜率分别为k1，k2，若对任意k，存在实数λ，使得k1+ k2=λk，求实数λ的取值范围.

    查看答案和解析>>

    同步练习册答案