
在△ABC中,a,b,c分别为内角A,B,C的对边,且2asin A=(2b+c)sin B+(2c+b)sin C.
(1)求A的大小;
(2)若sin B+sin C=1,试判断△ABC的形状.
解 (1)由已知,根据正弦定理得2a2=(2b+c)b+(2c+b)c,
即a2=b2+c2+bc.
由余弦定理得a2=b2+c2-2bccos A,
故cos A=- ,A=120°.
,A=120°.
(2)方法一 由(1)得sin2A=sin2B+sin2C+sin Bsin C,
又A=120°,∴sin2B+sin2C+sin Bsin C=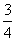 ,
,
∵sin B+sin C=1,∴sin C=1-sin B.
∴sin2B+(1-sin B)2+sin B(1-sin B)=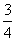 ,
,
即sin2B-sin B+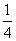 =0.
=0.
解得sin B= .故sin C=
.故sin C= .
.
∴B=C=30°.
所以,△ABC是等腰的钝角三角形.
方法二 由(1)A=120°,∴B+C=60°,
则C=60°-B,
∴sin B+sin C=sin B+sin(60°-B)
=sin B+ cos B-
cos B- sin B
sin B
= sin B+
sin B+ cos B
cos B
=sin(B+60°)
=1,
∴B=30°,C=30°.
∴△ABC是等腰的钝角三角形.


科目:高中数学 来源: 题型:
在△ABC中,内角A,B,C的对边分别是a,b,c.若a2-b2=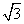 bc,
bc,
sin C=2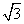 sin B,则A等于( )
sin B,则A等于( )
A.30° B.60°
C.120° D.150°
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,如果sin Asin B+sin Acos B+cos Asin B+cos Acos B=2,则△ABC是( )
A.等边三角形 B.钝角三角形
C.等腰直角三角形 D.直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
在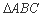 中,有如下四个命题:①
中,有如下四个命题:① ; ②
; ②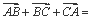
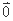 ;③若
;③若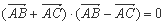 ,则
,则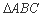 为等腰三角形;④若
为等腰三角形;④若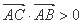 ,则
,则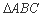 为锐角三角形.其中正确的命题序号是( )
为锐角三角形.其中正确的命题序号是( )
A.① ② B.① ③ ④ C.② ③ D.② ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com