练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，AB＝7，AC＝6，M是BC的中点，AM＝4，则BC等于(　　)

    A.                   B.

    C.                   D.


    B

    解析　设BC＝a，则BM＝MC＝.

    在△ABM中，AB2＝BM 2＋AM 2－2BM·AM·cos∠AMB，

    即72＝a2＋42－2××4·cos∠AMB             ①

    在△ACM中，AC2＝AM 2＋CM 2－2AM·CM·cos∠AMC

    即62＝42＋a2＋2×4×·cos∠AMB            ②

    ①＋②得：72＋62＝42＋42＋a2，∴a＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若cos 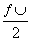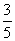＝，sin 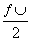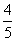＝－，则角θ的终边所在的直线方程为(　　)

    A．7x＋24y＝0        B．7x－24y＝0

    C．24x＋7y＝0        D．24x－7y＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某公司一年购买某种货物400吨，每次都购买x吨，运费为4万元/次，一年的总存储费用为4x万元，要使一年的总运费与总存储费用之和最小，则x＝________吨．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，已知(a＋b＋c)(b＋c－a)＝3bc，且sin A＝2sin Bcos C，试确定△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    根据下列情况，判断三角形解的情况，其中正确的是(　　)

    A．a＝8，b＝16，A＝30°，有两解

    B．b＝18，c＝20，B＝60°，有一解

    C．a＝5，c＝2，A＝90°，无解

    D．a＝30，b＝25，A＝150°，有一解

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A、B、C的对边分别为a、b、c，若a2＋c2－b2＝ac，则角B

    的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，a，b，c分别为内角A，B，C的对边，且2asin A＝(2b＋c)sin B＋(2c＋b)sin C.

    (1)求A的大小；

    (2)若sin B＋sin C＝1，试判断△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A、B、C所对的边分别为a、b、c.若(b－c)cos A＝acos C，则cos A＝________.

      

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设数列的前项和为，令，称为数列的“理想数”，已知数列的“理想数”为101，那么数列的“理想数”为____________．

    查看答案和解析>>

    同步练习册答案