
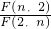 (n∈N*),求函数f(n)的最小值;
(n∈N*),求函数f(n)的最小值;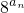 ,求数列{an}的通项公式,并求所有可能乘积aiaj(1≤i≤j≤n)的和.
,求数列{an}的通项公式,并求所有可能乘积aiaj(1≤i≤j≤n)的和.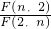 =
= ,
, =
=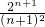
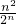 =
= ,
, ;…(6分)
;…(6分)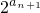 ,
,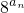 =
=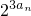 ,
,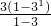 •31+
•31+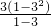 •32+…+
•32+…+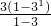 •3n
•3n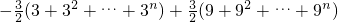
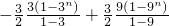
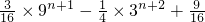 …(14分).
…(14分).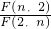 =
= ,要求f(n)的最小值,只要判断f(n)的单调性,利用比较法中的比商:
,要求f(n)的最小值,只要判断f(n)的单调性,利用比较法中的比商: =
= ,只要判断2n2与(n+1)2的大小即可判断
,只要判断2n2与(n+1)2的大小即可判断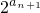 ,结合g(an+1)=
,结合g(an+1)=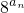 =
=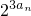 ,可得an+1与an的递推关系,进而可求通项,设所求的和为S,则S=a1•a1+(a1+a2)•a2+…+(a1+a2+…+an)•an利用分组求和的可求
,可得an+1与an的递推关系,进而可求通项,设所求的和为S,则S=a1•a1+(a1+a2)•a2+…+(a1+a2+…+an)•an利用分组求和的可求

科目:高中数学 来源: 题型:
| x-y |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
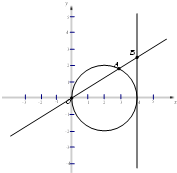 (2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足
(2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足| OM |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-y |
| A、① | B、② | C、③ | D、④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com