
A. | B.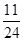 | C. | D. |
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:不详 题型:解答题
| API |  |  |  |  |  |  | 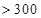 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
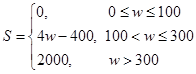 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率; 列联表,并判断能否有
列联表,并判断能否有 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关? | 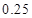 | 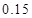 |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |  |

| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 投篮次数n | 8 | 10 | 12 | 9 | 10 | 16 |
| 进球次数m | 6 | 8 | 9 | 7 | 7 | 12 |
| 进球频率m/n | | | | | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,P(X=x2)=
,P(X=x2)= ,且x1<x2,又已知E(X)=
,且x1<x2,又已知E(X)= ,D(X)=
,D(X)= ,则x1+x2的值为( )
,则x1+x2的值为( )A. | B. | C.3 | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
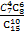 的是( )
的是( )| A.P(X=2) | B.P(X≤2) |
| C.P(X=4) | D.P(X≤4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com