练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设a,b,c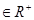,P=a+b-c,Q=b+c-a,R=a+c-b,则“PQR>0”是“P,Q,R”同时大于零的（     ）。

    A. 充分不必要条件      B. 必要不充分条件

    C. 充要条件            D. 既不充分也不必要条件

     

    【答案】

    C

    【解析】解：因为“PQR>0”包括了两个同负，和一个为正数，或者三个都为正，都可以得到P,Q，R为正数，但是前者显然不成立，矛盾。因此选择C

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•烟台二模）为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
    喜爱打篮球 不喜爱打篮球 合计
    男生 5
    女生 10
    合计 50
    已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
    3
    5
    ．
    （1）请将上面的列联表补充完整（不用写计算过程）；
    （2）能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关？说明你的理由；
    （3）现从女生中抽取2人进一步调查，设其中喜爱打篮球的女生人数为ξ，求ξ的分布列与期望．
    下面的临界值表供参考：
    P（K2≥k） 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
    （参考公式：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    设A(－c，0)，B(c，0)(c＞0)为两定点，动点P到A点的距离与到B点的距离的比为定值a(a＞0)，求P点的轨迹．

    查看答案和解析>>

    科目：高中数学 来源：2010年普通高等学校招生全国统一考试、理科数学A卷(广东卷) 题型：044

    设A(x1，y2)，B(x2，y2)是平面直角坐标系xOy上的两点，现定义由点A到点B的一种折线距离P(A，B)为P(A，B)＝｜x2－x1｜＋｜y2－y1｜对于平面xOy上给定的不同的两点A(x1，y2)，B(x2，y2)，

    (1)若点C(x，y)是平面xOy上的点，试证明p(A，C)＋p(C，B)≥p(A，B)

    (2)在平面xOy上是否存在点C(x，y)，同时满足

    ①p(A，C)＋p(C，B)＝p(A，B)

    ②p(A，C)＝p(C，B)

    若存在，请求出所有符合条件的点，请予以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    △ABC的边BC、CA、AB的中点分别为A1、B1、C1，任取一点O，OA、OB、OC的中点分别为A2、B2、C2，A1A2、B1B2、C1C2的中点分别为P、Q、R且设=a,=b,=c.用a、b、c分别表示、、，并判断P、Q、R三点的位置关系.

    查看答案和解析>>

    同步练习册答案