
分析 (1)容易看出定义域为R,而根据|x|≥0,便可得出$0<(\frac{2}{3})^{|x|}≤1$,这样便求出了该函数的值域;
(2)定义域为R,配方得到y=(2x+1)2,从而由2x>0可以得出2x+1的范围,进一步便可得出y的范围,即得出该函数的值域.
解答 解:(1)定义域为R;
|x|≥0;
∴$0<(\frac{2}{3})^{|x|}≤(\frac{2}{3})^{0}=1$;
∴该函数的值域为(0,1];
(2)定义域为R;
y=4x+2•2x+1=(2x+1)2;
2x>0;
∴2x+1>1;
∴y>1;
∴该函数的值域为(1,+∞).
点评 考查函数定义域、值域的概念及求法,指数函数的单调性,指数函数的值域,以及配方法处理二次式子.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
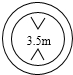 图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )| A. | h≤3.5 | B. | h≥3.5 | C. | h<3.5 | D. | h>3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | t∉M | B. | t+2∈M | C. | t+1∈M | D. | t-1∉M |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com