
����Ŀ�����ڣ�����ʡ�人�еȶ��������������״������Ⱦ�ķ������飮Ϊ�˾������ס���飬�ҹ����й��������ڿ���һ�ߣ��Ӱ�ӵ����ֶ����벡��������ҹ�Լ��յؽ����о�������״������DZ���ڼ����������ƵĹؼ�����֮һ���ڴ�Ⱦ��ѧ�У�ͨ���Ѵ��²��̼�����������Ի��巢�������𣬵�������ַ�Ӧ��ʼ���ָü�����Ӧ�����֢״ʱֹ����һ�γ�ΪDZ���ڣ�����ɽԺʿ������о��Ŷ�ͳ�����人��ij����10000��ҽѧ�۲��ߵ������Ϣ����ͨ�������Ӻ�����õ�1000��ȷ�ﻼ�ߵ���Ϣ���±���
DZ���ڣ���λ���죩 |
|
|
|
|
���� | 800 | 190 | 8 | 2 |
��1������1000��ȷ�ﻼ�ߵ�DZ�����������ݵ�ƽ����![]() ��ͬһ�������ø�������������е�ֵ��������
��ͬһ�������ø�������������е�ֵ��������
��2������״������DZ�������������Ӱ�죬Ϊ���о�DZ�����뻼���Ա�Ĺ�ϵ����DZ�����Ƿ�7��Ϊ�����зֲ������������1000�������г�ȡ100�����õ��������������뽫�����������������������������ж��Ƿ���90%�İ�����ΪDZ�����뻼���Ա��йأ�
DZ������7�� | DZ����>7�� | �ܼ� | |
���Ի��� | 12 | ||
Ů�Ի��� | 50 | ||
�ܼ� | 100 |
��3�����ڲ��������걾���治�����ò�ͬ���͵ı걾�Լ�ʹ�ò�ͬ�����Լ���������ɺ�����������������������©��������������ʱ����Ҫ��һ������Ѫ��ѧ![]() �����⣬���ֲ�������©���ȱ�㣮�ֶ�10���������������Ե���Ա��һ�ؽ���Ѫ���⣬��ÿ���˼���
�����⣬���ֲ�������©���ȱ�㣮�ֶ�10���������������Ե���Ա��һ�ؽ���Ѫ���⣬��ÿ���˼���![]() ��
��![]() �ǽ��ڸ�Ⱦ�ı�־�������Եĸ���Ϊ
�ǽ��ڸ�Ⱦ�ı�־�������Եĸ���Ϊ![]() ��������������ټ����9���˲ż���
��������������ټ����9���˲ż���![]() �����Եĸ���Ϊ
�����Եĸ���Ϊ![]() ����
����![]() ȡ�����ֵʱ��Ӧ�ĸ���
ȡ�����ֵʱ��Ӧ�ĸ���![]() ��
��
����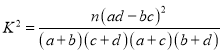 ������
������![]() ��
��
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1��4.984�죨2����������������90%�İ�����ΪDZ�����뻼�������й�.��3��![]()
��������
��1������ƽ�����ļ��㷽���������ƽ����.
��2��������֪������д![]() �������������
�������������![]() ���ɴ��жϳ�������90%�İ�����ΪDZ�����뻼�������й�.
���ɴ��жϳ�������90%�İ�����ΪDZ�����뻼�������й�.
��3�����![]() �ı���ʽ�����õ������
�ı���ʽ�����õ������![]() ȡ�����ֵʱ��
ȡ�����ֵʱ��![]() ��ֵ.
��ֵ.
��1��![]() ��
��
��2��
DZ����<7�� | DZ������7�� | �ܼ� | |
���Ի��� | 38 | 12 | 50 |
Ů�Ի��� | 42 | 8 | 50 |
�ܼ� | 80 | 20 | 100 |
��![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]()
�����90%�İ�����ΪDZ�����뻼�������й�.
��3����![]() �������
�������![]()
��![]() ��
��![]() ����
����![]() ��
��
��![]()
��![]() ��
��![]() ����
����![]()
��![]() ����
����![]() ���
���![]() ����
����![]() �����
�����![]() ��
��
��![]() ��
��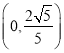 �ϵ�����������
�ϵ�����������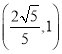 �ϵ����ݼ���
�ϵ����ݼ���
��![]() ��Ψһ�ļ���ֵΪ
��Ψһ�ļ���ֵΪ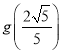 ��Ҳ�����ֵ.
��Ҳ�����ֵ.
�൱![]() ʱ����
ʱ����![]() ʱ��
ʱ��![]() ȡ�����ֵ��
ȡ�����ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������й����Իع�������ĸ����⣺
�����Իع�ֱ�߱ع��������ݵ����ĵ㣨![]() ����
����
�ڻع�ֱ�߾���ɢ��ͼ�о����������ݵ���������ֱ�ߣ�
�۵������ϵ��![]() ʱ��������������أ�
ʱ��������������أ�
��������������������Խǿ���������ϵ��![]() ��Խ�ӽ���
��Խ�ӽ���![]() ��
��
����������ĸ���Ϊ��������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʮ�Ŵ�Ҫ��ȷ����2020���ҹ����б���ũ��ƶ���˿�ʵ����ƶ��ƶ����ȫ��ժñ���������������ƶ������������ƶ������ƶ.ijƶ��������ƶ������᳹��ʵ���Ҿ���ƶ������Ҫ����ũ���������Ⱥ����ƶ��С������ƶ��ƻ�Ϊijũ���������ũ��������������ֻ���ʹ���������̭.ũ�����������̶Թ���û����Ŀͻ��Ƴ����������۷�����
����һ��ÿ̨�����ۼ�7000Ԫ�������ڿ���ѱ���2�Σ�����2��ÿ����ȡ������200Ԫ��
��������ÿ̨�����ۼ�7050Ԫ�������ڿ���ѱ���3�Σ�����3��ÿ����ȡ������100Ԫ.
��ƶ����Ҫ�����ڹ������ʱӦ��ѡȡ���ַ�����Ϊ���Ѽ���������50̨���ֻ���������ʹ�����ڱ����Ĵ��������±���
�������� | 0 | 1 | 2 | 3 | 4 | 5 |
̨�� | 1 | 10 | 19 | 14 | 4 | 2 |
��x��ʾ1̨����������ʹ�����ڵı�������.
��1�����������������˼�룬����x������3���ĸ��ʣ�
��2�������������۷������ֱ������50̨��������ʹ�����ڵ��ܷ��ã��ܷ���=�ۼ�+�����ѣ�����ÿ̨ÿ���ƽ��������Ϊ�������ݣ���ƶ��ѡ���������۷���������������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����![]() �У���
�У���![]() �ֱ�����
�ֱ�����![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��
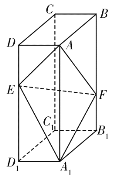
��1��֤������![]() ��ƽ��
��ƽ��![]() �ڣ�
�ڣ�
��2����![]() ��
��![]() ��
��![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��6��25�գ������������Ⱦ�������η�(���ݰ�)����������ȫ���˴�ί�����飬�ݰ��ԡ�����������Ⱦ�����ķ��Ρ�������ר��涨.ijС����ȡһϵ�д�ʩ���������������֪ʶ�����壬���ɹ�����������.Ϊ���˽����������Ч������С����ҵ�����ȡ��200λ��������ʾ����飬ÿλ�����С����ȡ�Ĵ�ʩ���������⡱�����⡱������.���ݵ�����ͳ�Ʋ���������ֲ�����ͼ�ͳֲ�����̬�ȵľ���Ľṹ����ͼ����ͼ������200���ʾ��У�������̬�ȵ�Ƶ����0.65.
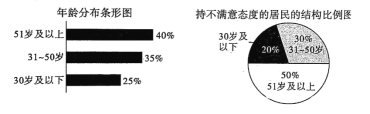
��1����������![]() �����������ж��ܷ���
�����������ж��ܷ���![]() �İ�����Ϊ��51�꼰���ϡ��͡�50�꼰���¡��ľ���Ը�С����ȡ�Ĵ�ʩ�������в���
�İ�����Ϊ��51�꼰���ϡ��͡�50�꼰���¡��ľ���Ը�С����ȡ�Ĵ�ʩ�������в���
���� | ������ | �ܼ� | |
51�꼰���ϵľ��� | |||
50�꼰���µľ��� | |||
�ܼ� | 200 |
��2������51�꼰���ϡ��͡�50�꼰���¡�������β�ȡ�ֲ�����ķ������������ȡ5�ݣ��ٴ���5�ݵ����ʾ��������ȡ2�ݽ��е绰�ҷã���绰�ҷõ���λ����ǡ��һλ������51�꼰���ϣ���һλ������50�꼰���µĸ���.
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�������ο���ʽ��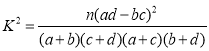 ������
������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ��������
��������![]() ��
��![]() ����
Ϊ����![]() �ϵ�һ����.
�ϵ�һ����.
��I����![]() ��Ӧ�IJ�����
��Ӧ�IJ�����![]() �䶯��
�䶯��![]() ʱ���߶�
ʱ���߶�![]() ��ɨ����ͼ�������
��ɨ����ͼ�������
������ֱ��![]() ������
������![]() ����һ������Ϊ
����һ������Ϊ![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣿�����ڣ������
���е㣿�����ڣ������![]() ���ꣻ�������ڣ�˵������.
���ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
��1����![]() �ڵ�
�ڵ�![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��2����![]() �ĵ������䣻
�ĵ������䣻
��3����![]() ����֤����
����֤����![]() ʱ��
ʱ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��l��������C��y2��4x�Ľ���F����C����A��x1��y1����B��x2��y2�����㣬��y1y2��_____����A��B����ֱ���������C���ߵĴ��ߣ�����ֱ�ΪP��Q������x��Ľ���ΪM���ı���FAPM�������ΪS1���ı���FBQM�������ΪS2����S1S2��3|AF||BF|��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��1��3���϶��ĺ�̽�����ɹ�ʵ��������ʷ���״�����������½���ҹ�������ҵȡ����һ�ش�ɾͣ�ʵ������������½��Ҫ�����һ���ؼ����������ǵ�����̽������ͨѶ��ϵ��Ϊ���������⣬�������϶��ĺ��м��ǡ�ȵ�š���ȵ������Χ�Ƶ�����������![]() ��Ĺ�����У�
��Ĺ�����У�![]() ����ƽ��㣬λ�ڵ������ߵ��ӳ����ϣ����������ΪM������������ΪM�������¾���ΪR��
����ƽ��㣬λ�ڵ������ߵ��ӳ����ϣ����������ΪM������������ΪM�������¾���ΪR��![]() �㵽����ľ���Ϊr������ţ���˶����ɺ������������ɣ�r���㷽�̣�
�㵽����ľ���Ϊr������ţ���˶����ɺ������������ɣ�r���㷽�̣�
![]() .
.
��![]() ������
������![]() ��ֵ��С������ڽ��Ƽ�����
��ֵ��С������ڽ��Ƽ�����![]() ����r�Ľ���ֵΪ
����r�Ľ���ֵΪ
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com