
已知直三棱柱ABCA1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( )
A.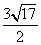 B.2
B.2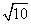 C.
C.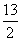 D.3
D.3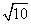
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知f(x)=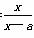 (x≠a).
(x≠a).
(1)若a=-2,试证f(x)在(-∞,-2)内单调递增;
(2)若a>0且f(x)在(1,+∞)内单调递减,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l,m,平面α,β,且l⊥α,m⊂β,则α∥β是l⊥m的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
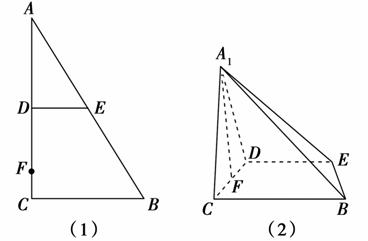
如图(1),在Rt△ABC中,∠C=90°,D,E分别为A C,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
C,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
(1)求证:DE∥平面A1CB.
(2)求证:A1F⊥BE.
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知一个半径为1的半球形容器①及容器②的三视图,侧视图矩形的宽为5,俯视图是边长为1的正三角形.
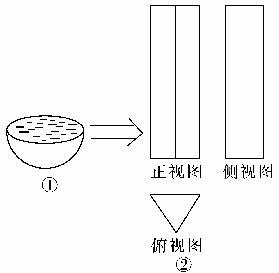
(1)请画出容器②的直观图(简图,尺寸不作严格要求),并回答:它是什么几何体?
(2)若把容器①中盛满的水全部注入容器②中,水是否会从容器②中溢出?为什么?(参考数据: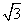 ≈1.732)
≈1.732)
查看答案和解析>>
科目:高中数学 来源: 题型:
正方体ABCDA1B1C1D1中,E、F分别是线段BC、C1D的中点,则直线A1B与直线EF的位置关系是( )
A.相交 B.平行
C.异面 D.以上都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
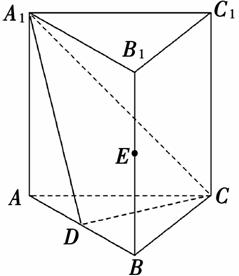
如图,直三棱柱ABCA1B1C1中, D,
D, E分别是AB,BB1的中点.
E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2 ,求三棱锥CA1DE的体积.
,求三棱锥CA1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
如果函数f(x)=ax+b-1(a>0,且a≠1)的图象经过第一、二、四象限,不经过第三象限,那么一定有( )
A.0<a<1且b>0
B.0<a<1且0<b<1
C.a>1且b<0
D.a>1且b> 0
0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com