
如图(1),在Rt△ABC中,∠C=90°,D,E分别为A C,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
C,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
(1)求证:DE∥平面A1CB.
(2)求证:A1F⊥BE.
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
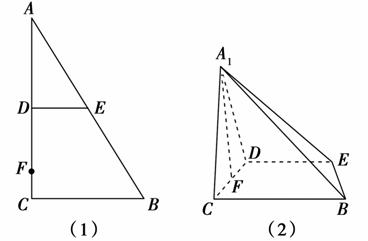
(1)证明:∵D,E分别为AC,AB的中点,∴DE∥BC.
又DE⊄平面A1CB,∴DE∥平面A1CB.
(2)证明:由已知得AC⊥BC且DE∥BC,
∴DE⊥AC.
∴DE⊥A1D,DE⊥CD.
∴DE⊥平面A1DC.
而A1F⊂平面A1DC,∴DE⊥A1F.
又A1F⊥CD,
∴A1F⊥平面BCDE.∴A1F⊥BE.
(3)解析:线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如下图,分别取A1C,A1B的中点P,Q,则PQ∥BC.
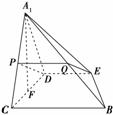
又DE∥BC,∴DE∥PQ.∴平面DEQ即为平面DEP.
由(2)知,DE⊥平面A1DC,∴DE⊥A1C.
又P是等腰三角形DA1C底边A1C的中点,∴A1C⊥DP.∴A1C⊥平面DEP.从而A1C⊥平面DEQ.
故线段A1B上存在点Q,使得A1C⊥平面DEQ.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a,b]上有
( )
A.最小值f(a) B.最大值f(b)
C.最小值f(b) D.最大值f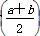
查看答案和解析>>
科目:高中数学 来源: 题型:
若m,n是互不相同的空间直线,α是平面,则下列命题中正确的是( )
A.若m∥n,n⊂α,则m∥α B.若m∥n,n∥α,则m∥α
C.若m∥n, n⊥α,则m⊥α D.若m⊥n,n⊥α,则m⊥α
n⊥α,则m⊥α D.若m⊥n,n⊥α,则m⊥α
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直三棱柱ABCA1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( )
A.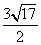 B.2
B.2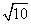 C.
C.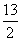 D.3
D.3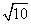
查看答案和解析>>
科目:高中数学 来源: 题型:
过三点确定一个平面
②梯形可以确定一个平面
③两两相交的三条直线最多可以确定三个平面
④如果 两个平面有三个公共点,则这两个平面重合.
两个平面有三个公共点,则这两个平面重合.
A.1  B.2 C.3 D.4
B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com