
【题目】已知函数![]() ,且定义域为
,且定义域为![]() .
.
(1)求关于![]() 的方程
的方程![]() 在
在![]() 上的解;
上的解;
(2)若![]() 在区间
在区间![]() 上单调减函数,求实数
上单调减函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的实根,求实数
上有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,则下列结论中正确结论的序号是__________.
,则下列结论中正确结论的序号是__________.
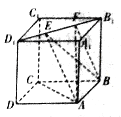
①![]() ;
;
②直线![]() 与平面
与平面![]() 所成角的正弦值为定值
所成角的正弦值为定值![]() ;
;
③当![]() 为定值,则三棱锥
为定值,则三棱锥![]() 的体积为定值;
的体积为定值;
④异面直线![]() 所成的角的余弦值为定值
所成的角的余弦值为定值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若学生![]() 一天学习数学超过两个小时的概率为
一天学习数学超过两个小时的概率为![]() (每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(Ⅰ)①设学生![]() 本周一天学习数学超过两个小时的天数为
本周一天学习数学超过两个小时的天数为![]() 求
求![]() 的分布列与数学期望
的分布列与数学期望![]()
②求学生![]() 本周数学学习投入的概率.
本周数学学习投入的概率.
(Ⅱ)为了研究学生学习数学的投入程度和本周数学周练成绩的关系,随机在年级中抽取了![]() 名学生进行调查,所得数据如下表所示:
名学生进行调查,所得数据如下表所示:
成绩理想 | 成绩不太理想 | 合计 | |
数学学习投入 | 20 | 10 | 30 |
数学学习不太投入 | 10 | 15 | 25 |
合计 | 30 | 25 | 55 |
根据上述数据能否有![]() 的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
附:![]()
|
|
|
|
|
|
|
|
|
|
| 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面ABCD为菱形,且∠ABC=60°,
AB=PC=2,PA=PB= ![]() .
.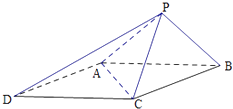
(1)求证:平面PAB⊥平面ABCD;
(2)设H是PB上的动点,求CH与平面PAB所成最大角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
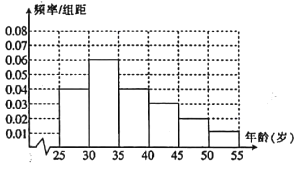
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取1000人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取1000人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁、
岁、![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的80%、60%.
岁年龄段人数中,“时尚族”人数分别占本组人数的80%、60%.
请完成以下问题:
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队,求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队,求领队的两人年龄都在![]() 岁内的概率.
岁内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)判断函数f(x)的奇偶性;
(2)判断并用定义证明函数f(x)在其定义域上的单调性.
(3)若对任意的t![]() 1,不等式f(
1,不等式f(![]() )+f(
)+f(![]() )<0恒成立,求k的取值范围.
)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣lnx.
(参考数据:e≈2.718,ln2≈0.693,ln3≈1.099,ln5≈1.609,ln7≈1.946)
(1)求证:函数f(x)有且只有一个极值点x0;
(2)求函数f(x)的极值点x0的近似值x′,使得|x′﹣x0|<0.1;
(3)求证:f(x)>2.3对x∈(0,+∞)恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com