
| x2 |
| 4 |
| x2 |
| 4 |
| a2-b2 |
| 3 |
| c |
| a |
| 8k2m |
| 1+4k2 |
| 4k2m2-4 |
| 1+4k2 |
| (1+k2)[(x1+x2)2-4x1x2] |
| x2 |
| 4 |
| a2-b2 |
| 3 |
| 3 |
| c |
| a |
| ||
| 2 |
| |km| | ||
|
|
| 4 |
| m2-1 |
| m2 |
| m2-1 |
|
|
| 3 |
| 3 |
| 8k2m |
| 1+4k2 |
| 4k2m2-4 |
| 1+4k2 |
| (1+k2)[(x1+x2)2-4x1x2] |
(1+k2)[
|
4
| ||
| m2+3 |
4
| ||
|m|+
|
| 3 |


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
| 2n-1 |
| (an+1)(an+1+1) |
| 1 |
| 15 |
| 1 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 10 | |
| [39.97,39.99) | 20 | |
| [39.99,40.01) | 50 | |
| [40.01,40.03] | 20 | |
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
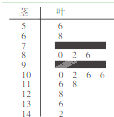 某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:| 分数段(分) | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] | 合计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、8 | B、9 | C、10 | D、11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com