
 在平面直角坐标系xOy中,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点($\sqrt{2}$,1),过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
在平面直角坐标系xOy中,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,且经过点($\sqrt{2}$,1),过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.分析 (Ⅰ)由已知$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,又$\frac{2}{a^2}+\frac{1}{b^2}=1$,a2=b2+c2.联立解得即可得出椭圆C的方程.
(Ⅱ)由(Ⅰ)知,A(-2,0),B(2,0),直线BM斜率显然存在,设BM方程为y=k(x-2),则M(-2,-4k),与椭圆方程联立化为(2k2+1)x2-8k2+8k2-4=0,△>0,利用根与系数的关系,只要证明$\overrightarrow{AP}•\overrightarrow{OM}$=0即可.
(Ⅲ)利用数量积运算性质即可得出.
解答 (Ⅰ)解:由已知$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,又$\frac{2}{a^2}+\frac{1}{b^2}=1$,∴a2=b2+c2.
联立解得:a2=4,b2=2.
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(Ⅱ)证明:由(Ⅰ)知,A(-2,0),B(2,0),直线BM斜率显然存在,
设BM方程为y=k(x-2),则M(-2,-4k),
由$\left\{\begin{array}{l}y=k(x-2)\\ \frac{x^2}{4}+\frac{y^2}{2}=1\end{array}\right.$,得(2k2+1)x2-8k2+8k2-4=0,△>0,
则$2{x_P}=\frac{{8{k^2}-4}}{{2{k^2}+1}}$,∴${x_P}=\frac{{4{k^2}-2}}{{2{k^2}+1}}$,${y_P}=k({x_P}-2)=\frac{-4k}{{2{k^2}+1}}$,即$P(\frac{{4{k^2}-2}}{{2{k^2}+1}},\frac{-4k}{{2{k^2}+1}})$.
又$\overrightarrow{AP}=(\frac{{8{k^2}}}{{2{k^2}+1}},\frac{-4k}{{2{k^2}+1}})$,$\overrightarrow{OM}=(-2,-4k)$,
∴$\overrightarrow{AP}•\overrightarrow{OM}=\frac{{-16{k^2}}}{{2{k^2}+1}}+\frac{{16{k^2}}}{{2{k^2}+1}}=0$,即AP⊥OM.
(Ⅲ)解:$\overrightarrow{OP}•\overrightarrow{OM}=(\frac{{4{k^2}-2}}{{2{k^2}+1}},\frac{-4k}{{2{k^2}+1}})•(-2,-4k)=\frac{{-8{k^2}+4+16{k^2}}}{{2{k^2}+1}}=\frac{{8{k^2}+4}}{{2{k^2}+1}}=4$,
∴$\overrightarrow{OP}•\overrightarrow{OM}$为定值4.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次的根与系数的关系、向量垂直于数量积的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 9月5日 | 10月3日 | 10月8日 | 11月16日 | 12月21日 |
| 气温x(℃) | 18 | 15 | 11 | 9 | -3 |
| 用水量y(吨) | 69 | 57 | 45 | 47 | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y3>y1>y2 | B. | y2>y1>y3 | C. | y1>y2>y3 | D. | y1>y3>y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
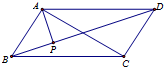 如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AB}$+$\overrightarrow{AP}$•$\overrightarrow{AD}$=8.
如图,在平行四边形ABCD中,AP⊥BD,垂足为P,且AP=2,则$\overrightarrow{AP}$•$\overrightarrow{AB}$+$\overrightarrow{AP}$•$\overrightarrow{AD}$=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com