
| A. | (-1,1) | B. | (1,$\frac{π}{2}$) | C. | (0,$\frac{π}{2}$) | D. | (-1,$\frac{π}{2}$) |
分析 令g(x)=cosx+xsinx,利用导数判断g(x)在[-π,π]上的单调性和极值,区间端点值,根据零点个数判断m的范围.
解答 解:令f(x)=0得cosx+xsinx=m,
令g(x)=cosx+xsinx,则g′(x)=-sinx+sinx+xcosx=xcosx.
令g′(x)=0得x=0或cosx=0,
∴x=0或x=$\frac{π}{2}$+kπ,k∈Z.
∴g(x)在[-π,π]上随x的变化如下表所示:
| x | [-π,-$\frac{π}{2}$) | -$\frac{π}{2}$ | (-$\frac{π}{2}$,0) | 0 | (0,$\frac{π}{2}$) | $\frac{π}{2}$ | ($\frac{π}{2}$,π] |
| g′(x) | + | 0 | - | 0 | + | 0 | - |
| g(x) | 增函数 | 极大值 | 减函数 | 极小值 | 增函数 | 极大值 | 减函数 |
点评 本题考查了导数与函数单调性的关系,零点个数与极值的关系,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
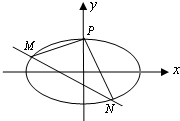 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且过点P(0,1).
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,且过点P(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{e}$ | B. | $\frac{2}{e}$ | C. | $\frac{2\sqrt{e}}{e}$ | D. | $\frac{\sqrt{e}}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{2}}{2}$] | B. | ($\frac{\sqrt{3}}{3}$,1) | C. | (0,$\frac{\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{2}}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
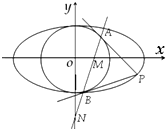 已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com