
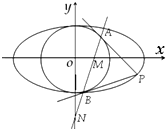
 ��֪��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0����ԲO��x2+y2=b2������Բ��һ��P��ԲO���������ߣ��е�ֱ�ΪA��B��
��֪��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0����ԲO��x2+y2=b2������Բ��һ��P��ԲO���������ߣ��е�ֱ�ΪA��B������ ������ԲO����Բ�Ľ��㣬ԲO��x2+y2=b2���ɵ�b=c��������b2=a2-c2�����������ʼ��㹫ʽ���ɵó���
������P��x0��y0����A��x1��y1����B��x2��y2�����������ߵ����ʿɵã�$\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}$=-$\frac{{x}_{1}}{{y}_{1}}$�����������õ�PA����Ϊ��x1x0+y1y0=b2��ͬ���ɵã�PB����Ϊ��x2x0+y2y0=b2���ɵ�ֱ��AB�ķ���Ϊ��x0x+y0y=b2��������${b}^{2}{x}_{0}^{2}$+${a}^{2}{y}_{0}^{2}$=a2b2�����ɵó���ֵ��
��� �⣺����ԲO����Բ�Ľ��㣬ԲO��x2+y2=b2����b=c��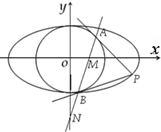
��b2=a2-c2��a2=2c2����e=$\frac{\sqrt{2}}{2}$��
������P��x0��y0����A��x1��y1����B��x2��y2����
��$\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}$=-$\frac{{x}_{1}}{{y}_{1}}$��������x0x1+y0y1=${x}_{1}^{2}$+${y}_{1}^{2}$��
��${x}_{1}^{2}$+${y}_{1}^{2}$=b2����PA������x1x0+y1y0=b2��
ͬ���ɵã�PB����Ϊ��x2x0+y2y0=b2��
�Ӷ�ֱ��AB�ķ���Ϊ��x0x+y0y=b2��
��x=0����|ON|=|y|=$\frac{{b}^{2}}{|{y}_{0}|}$����y=0����|OM|=|x|=$\frac{{b}^{2}}{|{x}_{0}|}$��
��$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$=1����${b}^{2}{x}_{0}^{2}$+${a}^{2}{y}_{0}^{2}$=a2b2��
��$\frac{a^2}{{O{N^2}}}$+$\frac{b^2}{{O{M^2}}}$=$\frac{{a}^{2}{y}_{0}^{2}+{b}^{2}{x}_{0}^{2}}{{b}^{4}}$=$\frac{{a}^{2}{b}^{2}}{{b}^{4}}$=$\frac{{a}^{2}}{{b}^{2}}$��
��$\frac{a^2}{{O{N^2}}}$+$\frac{b^2}{{O{M^2}}}$=$\frac{{a}^{2}}{{b}^{2}}$Ϊ��ֵ��
���� ���⿼������Բ�ı����̼������ʡ�ֱ����Բ���е����ʡ�б�ʼ��㹫ʽ��������Բ��λ�ù�ϵ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��1�� | B�� | ��1��$\frac{��}{2}$�� | C�� | ��0��$\frac{��}{2}$�� | D�� | ��-1��$\frac{��}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}$ | B�� | 2 | C�� | $\sqrt{3}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | -$\frac{1}{4}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | c��a��b | B�� | c��b��a | C�� | a��b��c | D�� | a��c��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com