
分析 (1)由acosA=bcosB,利用正弦定理可得:sin2A=sin2B,2A,2B∈(0,2π).由于a≠b,可得A≠B,可得A+B=$\frac{π}{2}$.即可得出C.
(2)由sinB=cosA 得y=$\frac{sinA+cosA}{sinAcosA}$,令 sinA+cosA=t∈(1,$\sqrt{2}$],则 sinAcosA=$\frac{{t}^{2}-1}{2}$,y=$\frac{2t}{{t}^{2}-1}$=$\frac{2}{t-\frac{1}{t}}$,根据t-$\frac{1}{t}$在(1,$\sqrt{2}$]单调递增,即可求得实数y的取值范围.
解答 (本题满分为14分)
解:(1)∵acosA=bcosB,
∴sinAcosA=sinBcosB,
∴sin2A=sin2B,2A,2B∈(0,2π).
∴2A=2B,或2A=π-2B,
∵a≠b,∴A≠B,
∴A+B=$\frac{π}{2}$.
∴C=π-(A+B)=$\frac{π}{2}$.…(6分)
(2)∵sinB=cosA,
∴y=$\frac{sinA+cosA}{sinAcosA}$,…(7分)
∵sinA+cosA=$\sqrt{2}$sin(A+$\frac{π}{4}$),A∈(0,$\frac{π}{2}$),
∴A+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{4}$).
∴sin(A+$\frac{π}{4}$)∈($\frac{\sqrt{2}}{2}$,1],
∴sinA+cosA∈(1,$\sqrt{2}$],…(9分)
令 sinA+cosA=t∈(1,$\sqrt{2}$],则 sinAcosA=$\frac{{t}^{2}-1}{2}$,…(11分)
∴y=$\frac{2t}{{t}^{2}-1}$=$\frac{2}{t-\frac{1}{t}}$,…(12分)
∵t-$\frac{1}{t}$在(1,$\sqrt{2}$]单调递增,
∴0<t-$\frac{1}{t}$≤$\sqrt{2}$-$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴y≥2$\sqrt{2}$,
又a≠b,故等号不成立,
∴y的取值范围为(2$\sqrt{2}$,+∞)…(14分)
点评 本题考查了正弦定理、倍角公式、同角三角函数基本关系式、“弦化切”、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
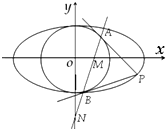 已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
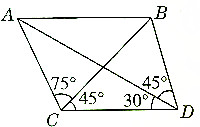 如图,在四边形ABDC中,CD=$\sqrt{3}$,∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求AB的长.
如图,在四边形ABDC中,CD=$\sqrt{3}$,∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com