考点:命题的真假判断与应用
专题:空间角,简易逻辑
分析:取正方体ABCD-A1B1C1D1,
①根据线线角的定义,结合正方体的12条棱,实际上就是三组平行直线,因此只要研究过一个顶点的三条棱即可,据此分析;
②同样的道理根据线面角的定义,结合六个表面,其实是三组平行平面,只需考虑过同一顶点的三个面即可;
③取平面A1C1B,可以判断,它与各棱所成的角都相等,要求该角的正弦值,只需研究正三棱锥B1-A1C1B即可;
④取平面A1C1B,可以判断,它与各面所成的锐角都相等,要求该角的正弦值,只需研究正三棱锥B1-A1C1B即可.
解答:
解:做出正方体ABCD-A
1B
1C
1D
1,
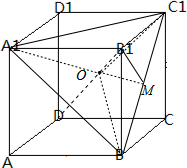
设正方体棱长为1.在正方体中连接DB
1,交平面A
1BC
1于O,易知DB
1⊥面A
1BC
1,且O是正三角形A
1BC
1的中心,连接A
1O并延长交BC
1于M,则M是BC
1的中点,连接B
1M,则B
1M⊥BC
1.
因此对于①,存在直线DB
1与各条棱所成的角相等,且在直角三角形A
1OB
1中,B
1O=
DB
1=
,
A1O=AM=×A1B=,∴tanα
1=
=,故①正确;
对于②,存在直线B
1D与各个面所成的角相等,则∠OB
1M就是所求,易知α
2=∠OB
1M=∠A
1B
1M,所以tanα
2=
=,故②正确;
对于③,∠B
1A
1O的大小就是平面A
1BC
1与所有12条棱所成的锐角的大小,在直角三角形A
1B
1M中,A
1M=
=,∴
sinα2==,故③正确;
对于④,存在平面A
1C
1B与各个面所成的二面角相等,且∠B
1MA
1就是所求角的平面角,易知sinα
4=
==,故④正确.
故答案为①②③④
点评:本题综合考查了线线角、线面角、二面角的概念及求法,并且有一定难度,注意先将所求的角转化为平面角再求解.



