
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极小值;
的极小值;
(2)设函数![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围,(
的取值范围,( ![]() )
)
【答案】(1)当![]() 时,函数
时,函数![]() 取得极小值1;(2)当
取得极小值1;(2)当![]() 时,
时, ![]() 的递减区间为
的递减区间为![]() ;递增区间为
;递增区间为![]() ,当
,当![]() 时,
时, ![]() 只有递增区间为
只有递增区间为![]() ;(3)
;(3) .
.
【解析】试题分析:本题主要考查导数的运算、利用导数判断函数的单调区间、利用导数求函数的极值和最值等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,当![]() 时,先得到
时,先得到![]() 解析式,在定义域范围内,解不等式
解析式,在定义域范围内,解不等式![]() ,
, ![]() 得到函数的单调区间,从而得到函数
得到函数的单调区间,从而得到函数![]() 的极值;第二问,先求出
的极值;第二问,先求出![]() 表达式,对
表达式,对![]() 求导,需讨论
求导,需讨论![]() 的根
的根![]() 与0的大小,分情况讨论;第三问,将在
与0的大小,分情况讨论;第三问,将在![]() (
(![]() )上存在一点
)上存在一点![]() ,使得
,使得![]() 成立转化为
成立转化为![]() ,构造函数
,构造函数![]() ,结合第二问的结论,讨论求
,结合第二问的结论,讨论求![]() 的最小值.
的最小值.
试题解析:(1)![]() 的定义域为
的定义域为![]() . 1分
. 1分
当![]() 时,
时, ![]() ,
, ![]() . 2分
. 2分
由![]() ,解得
,解得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
所以当![]() 时,函数
时,函数![]() 取得极小值,极小值为
取得极小值,极小值为![]() ; 4分
; 4分
(2)![]() ,其定义域为
,其定义域为![]() .
.
又![]() . 5分
. 5分
①当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,所以,函数
,所以,函数![]() 在
在![]() 上单调递增. 6分
上单调递增. 6分
②当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增; 7分
上单调递增; 7分
综上所述:当![]() 时,
时, ![]() 的递减区间为
的递减区间为![]() ;递增区间为
;递增区间为![]() .
.
当![]() 时,
时, ![]() 只有递增区间为
只有递增区间为![]() . 8分
. 8分
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,即在
成立,即在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() .
.
则函数![]() 在
在![]() 上的最小值小于零. 9分
上的最小值小于零. 9分
①当![]() ,即
,即![]() 时,由(2)可知
时,由(2)可知![]() 在
在![]() 上单调递减.
上单调递减.
故![]() 在
在![]() 上的最小值为
上的最小值为![]() ,由
,由![]() ,可得
,可得![]() .
.
因为![]() .所以
.所以![]() ; 10分
; 10分
②当![]() ,即
,即![]() 时,由(2)可知
时,由(2)可知![]() 在
在![]() 上单调递增.
上单调递增.
故![]() 在
在![]() 上最小值为
上最小值为![]() ,由
,由![]() ,
,
可得![]() (满足
(满足![]() ); 11分
); 11分
③当![]() ,即
,即![]() 时,由(2)可知可得
时,由(2)可知可得![]() 在
在![]() 上最小值为
上最小值为
![]() .
.
因为![]() ,所以,
,所以, ![]() .
.
![]()
![]() ,即
,即![]() 不满足题意,舍去. 13分
不满足题意,舍去. 13分
综上所述得![]() ,或
,或![]() .
.
![]() 实数
实数![]() 的取值范围为
的取值范围为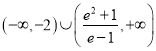 . 14分
. 14分


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(1)若![]() ,
, ![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,且
,且![]() ,求函数
,求函数![]() 在
在![]() 上的最小值及相应的
上的最小值及相应的![]() 值;
值;
(3)设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在研究某种药物对“H1N11”病毒的治疗效果时,进行动物试验,得到以下数据,对146只动物服用药物,其中101只动物存活,45只动物死亡;对照组144只动物进行常规治疗,其中124只动物存活,20只动物死亡.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)试问该种药物对治疗“H1N1”病毒是否有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合 计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合 计 | 70 | 30 | 100 |
⑴根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差
异”;
⑵已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机
抽取3人,求至多有1人喜欢甜品的概率.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
附: 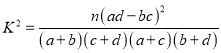 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)求![]() 的值;
的值;
(2)求函数![]() 的极小值;
的极小值;
(3)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com