
点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知平面α,β和直线m,给出下列条件:①m∥α;②m⊥α;③m?α;④α⊥β;⑤α∥β.
(1)当满足条件________时,有m∥β;
(2)当满足条件________时,有m⊥β(填所选条件的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 是两个不同的平面,
是两个不同的平面, 是平面
是平面 及
及 之外的两条不同直线,给出四个论断:
之外的两条不同直线,给出四个论断:
① ②
② ③
③ ④
④ 。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知下列命题:
①设m为直线, 为平面,且m
为平面,且m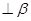 ,则“m//
,则“m// ”是“
”是“ ”的充要条件;
”的充要条件;
② 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;
③设随机变量 ~N(0,1),若P(
~N(0,1),若P( ≥2)=p,则P(-2<
≥2)=p,则P(-2< <0)=
<0)= ;
;
④若不等式|x+3|+|x-2|≥2m+1恒成立,则m的取值范围是( ,2);
,2);
⑤已知奇函数 满足
满足 ,且0<x<
,且0<x<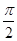 时
时 ,则函数
,则函数 在[
在[ ,
, ]上有5个零点.
]上有5个零点.
其中真命题的序号是 (写出全部真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设m、n是平面α外的两条直线,给出三个论断:
①m∥n;②m∥α;③n∥α.以其中的两个为条件,余下的一个为结论,构造三个命题,写出你认为正确的一个命题:________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com