
| A. | $\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=5+\frac{1}{2}t}\end{array}\right.$,(t为参数) | B. | $\left\{\begin{array}{l}{x=1-\frac{\sqrt{3}}{2}t}\\{y=5-\frac{1}{2}t}\end{array}\right.$,(t为参数) | ||
| C. | $\left\{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=5+\frac{\sqrt{3}}{2}t}\end{array}\right.$,(t为参数) | D. | $\left\{\begin{array}{l}{x=1-\frac{1}{2}t}\\{y=5+\frac{\sqrt{3}}{2}t}\end{array}\right.$,(t为参数) |
分析 根据题意,先写出直线的普通方程,再依次将选项的参数方程化为普通方程,与之比较即可得答案.
解答 解:根据题意,直线l经过点M(1,5)倾斜角为$\frac{π}{3}$,则直线的普通方程为y-5=$\sqrt{3}$(x-1),
据此依次分析选项:
对于A、将其参数方程化为普通方程为:y-5=$\frac{\sqrt{3}}{3}$(x-1),不符合题意,
对于B、将其参数方程化为普通方程为:y-5=-$\frac{\sqrt{3}}{3}$(x-1),不符合题意,
对于C、将其参数方程化为普通方程为:y-5=$\sqrt{3}$(x-1),符合题意,
对于D、将其参数方程化为普通方程为:y-5=-$\sqrt{3}$(x-1),不符合题意,
故选:C.
点评 本题考查直线的参数方程,关键是熟悉直线的参数方程的形式以及参数方程与普通方程的互化方法.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题

| A. | (13+3$\sqrt{7}$)cm2 | B. | (12+4$\sqrt{3}$)cm2 | C. | (18+3$\sqrt{7}$)cm2 | D. | $(9+3\sqrt{2}+3\sqrt{5})c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
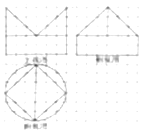 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )| A. | 9+16π | B. | 9+18π | C. | 12+18π | D. | 18+18π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{5\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com