
【题目】已知函数![]() 在
在![]() 与
与![]() 时都取得极值.
时都取得极值.
(1)求![]() 的值与函数
的值与函数![]() 的单调区间;
的单调区间;
(2)若对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】解:(1)![]() ……………………2分
……………………2分
由![]() ,
,
![]() ……………………3分
……………………3分
得![]() ……………………5分
……………………5分
(2)![]() ,
,
当![]() 时,
时,![]() 为极大值,……………………6分
为极大值,……………………6分
而![]() ,则
,则![]() 为最大值,……………………8分
为最大值,……………………8分
要使![]()
恒成立,则只需要![]() ,……………………10分
,……………………10分
得![]() ……………………12分
……………………12分
【解析】
(1)求出f![]() (x),由题意得f
(x),由题意得f![]() (
(![]() )=0且f
)=0且f![]() (1)=0联立解得
(1)=0联立解得![]() 与b的值,然后把
与b的值,然后把![]() 、b的值代入求得f(x)及f
、b的值代入求得f(x)及f![]() (x),讨论导函数的正负得到函数的增减区间;
(x),讨论导函数的正负得到函数的增减区间;
(2)根据(1)函数的单调性,由于x∈[﹣1,2]恒成立求出函数的最大值为f(2),代入求出最大值,然后令f(2)<c2列出不等式,求出c的范围即可.
(1)![]() ,f
,f![]() (x)=3x2+2ax+b
(x)=3x2+2ax+b
由 解得,
解得,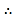
f![]() (x)=3x2﹣x﹣2=(3x+2)(x﹣1),函数f(x)的单调区间如下表:
(x)=3x2﹣x﹣2=(3x+2)(x﹣1),函数f(x)的单调区间如下表:
x | (﹣∞, |
| ( | 1 | (1,+∞) |
f | + | 0 | ﹣ | 0 | + |
f(x) |
| 极大值 |
| 极小值 |
|
所以函数f(x)的递增区间是(﹣∞,![]() )和(1,+∞),递减区间是(
)和(1,+∞),递减区间是(![]() ,1).
,1).
(2)因为![]() ,根据(1)函数f(x)的单调性,
,根据(1)函数f(x)的单调性,
得f(x)在(﹣1,![]() )上递增,在(
)上递增,在(![]() ,1)上递减,在(1,2)上递增,
,1)上递减,在(1,2)上递增,
所以当x![]() 时,f(x)
时,f(x)![]()
![]() 为极大值,而f(2)=
为极大值,而f(2)=![]() ,所以f(2)=2+c为最大值.
,所以f(2)=2+c为最大值.
要使f(x)<![]() 对x∈[﹣1,2]恒成立,须且只需
对x∈[﹣1,2]恒成立,须且只需![]() >f(2)=2+c.
>f(2)=2+c.
解得c<﹣1或c>2.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】某公司将进货单价为8元一个的商品按10元一个出售,每天可以卖出100个,若这种商品的售价每个上涨1元,则销售量就减少10个.
(1)求售价为13元时每天的销售利润;
(2)求售价定为多少元时,每天的销售利润最大,并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合Z={(x,y)|x∈[0,2],y∈[-1,1]}.
(1)若x,y∈Z,求x+y≥0的概率;
(2)若x,y∈R,求x+y≥0的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
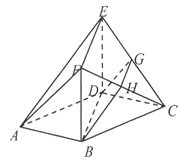
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,直线
时,直线![]() 与
与![]() 相切,求
相切,求![]() 的值;
的值;
(2)若函数![]() 在
在![]() 内有且只有一个零点,求此时函数
内有且只有一个零点,求此时函数![]() 的单调区间;
的单调区间;
(3)当![]() 时,若函数
时,若函数![]() 在
在![]() 上的最大值和最小值的和为1,求实数
上的最大值和最小值的和为1,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
说明你的理由;

(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com