
| A. | y=sin(4x+$\frac{π}{3}$) | B. | y=sin(x-$\frac{2π}{3}$) | C. | y=sin4x | D. | y=-sin4x |
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
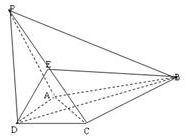 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 25 | ||
| 学习积极性一般 | 25 | ||
| 合计 | 24 | 26 | 50 |
| P(K2≥K0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b都能被5整除 | B. | a,b有1个不能被5整除 | ||
| C. | a不能被5整除 | D. | a,b都不能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -34 | B. | 34 | C. | 55 | D. | -55 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}+\overrightarrow{BA}=2\overrightarrow{AB}$ | B. | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CA}$ | C. | $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ | D. | $\overrightarrow{AB}-\overrightarrow{AD}-\overrightarrow{DC}=\overrightarrow{BC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 33 | C. | 30 | D. | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com