
分析 (1)根据题意和等差数列的定义,设一直角三角形的三边长分别为:a、a+2、a+4,再由直角三角形的面积公式和勾股定理求得a、d的值.
(2)利用(1)中求得的数据,根据等差数列的通项公式进行解答.
解答 解:(1)设一直角三角形的三边长分别为:a、a+d、a+2d,
则$\left\{\begin{array}{l}{\frac{1}{2}a(a+d)=6}\\{(a+2d)^{2}={a}^{2}+(a+d)^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=3}\\{d=1}\end{array}\right.$,
即d的值是1.
(2)设在以最短边的长为首项,公差为d的等差数列中,102为第n项,则
3+(n-1)×1=102,
解得n=100.
答:在以最短边的长为首项,公差为d的等差数列中,102为第100项.
点评 本题考查等差数列的定义,以及勾股定理的应用,属于基础题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(文)试卷(解析版) 题型:选择题
定义运算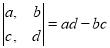 ,若
,若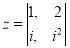 ,则复数
,则复数 对应的点在( )
对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 投掷序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 向上点数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生学科 | A | B | C | D | E |
| 数学成绩(x) | 88 | 76 | 73 | 66 | 63 |
| 化学成绩(y) | 78 | 65 | 71 | 64 | 61 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com