
分析 根据绝对值的应用,将函数进行转化,结合一元二次不等式与一元二次函数之间的关系,结合函数的单调性的性质进行讨论判断.
解答 解:解:令函数g(x)=x2-ax-2,由于g(x)的判别式△=a2+8>0,故函数g(x)一定有两个零点,
设为 x1 和x2,且 x1<x2.
∵函数f(x)=x2-|x2-ax-2|=$\left\{\begin{array}{l}{ax+2,}&{x<{x}_{1}或x>{x}_{2}}\\{2{x}^{2}-ax-2,}&{{x}_{1}≤x≤{x}_{2}}\end{array}\right.$,
故当x∈(-∞,x1)、(x2,+∞)时,
函数f(x)的图象是位于同一条直线上的两条射线,
当x∈(x1,x2 )时,函数f(x)的图象是抛物线y=2x2-ax-2下凹的一部分,且各段连在一起.
由于f(x)在区间(-∞,-1)和(2,+∞)上单调递增,
∴a>0且函数g(x)较小的零点x1=$\frac{a-\sqrt{{a}^{2}+8}}{2}$≥-1,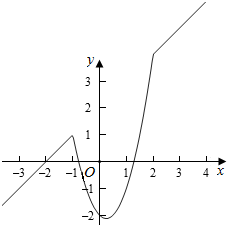
即a+2≥$\sqrt{{a}^{2}+8}$,
平方得a2+4a+4≥a2+8,得a≥1,
同时由y=2x2-ax-2的对称轴为 x=$-\frac{-a}{2×2}$=$\frac{a}{4}$,
若且-1≤$\frac{a}{4}$≤2,可得-4≤a≤8.
综上可得,1≤a≤8,
故实a的取值范围为[1,8],
故答案为:[1,8]
点评 本题主要考查函数单调性的应用,根据绝对值的意义转化为一元二次函数,利用一元二次函数和一元二次不等式之间的关系是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
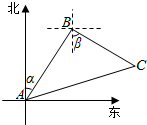 如图所示,一架飞机从A地沿北偏东35°的方向飞行800km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800km送往C地医院,求这架飞机飞行的路程及两次位移的和.
如图所示,一架飞机从A地沿北偏东35°的方向飞行800km到达B地接到受伤人员,然后又从B地按南偏东55°的方向飞行800km送往C地医院,求这架飞机飞行的路程及两次位移的和.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com