
(12分 ) .已知函数y=
) .已知函数y= f(x)=
f(x)=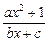 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<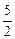
(1)试求函数f(x)的解析式
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说 明理由.
明理由.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
(本题满分16分)
设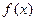 是定义在R上的奇函数,且对任意a、b
是定义在R上的奇函数,且对任意a、b ,当
,当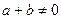 时,都有
时,都有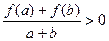 .
.
(1)若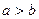 ,试比较
,试比较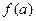 与
与 的大小关系;
的大小关系;
(2)若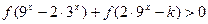 对任意
对任意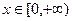 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某商品在近30天内每件的销售价格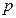 (元)与时间
(元)与时间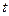 (天)的函数关系是
(天)的函数关系是 该商品的日销售量
该商品的日销售量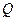 (件)与时间
(件)与时间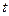 (天)的函数关系是
(天)的函数关系是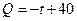
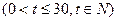 ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几 天?
天?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,现有一块矩形空地,要在这块空地上开辟一个内
如图,现有一块矩形空地,要在这块空地上开辟一个内 接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知
接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知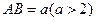 ,
,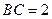 ,且
,且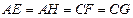 ,设
,设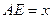 ,绿地面积为
,绿地面积为 .
.
1、写出 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
2、当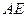 为何值时,绿地面积
为何值时,绿地面积 最大?
最大?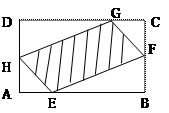
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)已知函数f(x)=ax+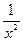 (x≠0,常数a∈R).
(x≠0,常数a∈R).
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数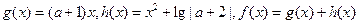 ,其中
,其中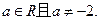
(1)若 为偶函数,求a的值;
为偶函数,求a的值;
(2)命题p:函数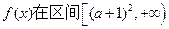 上是增函数,命题q:函数
上是增函数,命题q:函数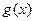 是减函数,如果p或q为真,p且q为假,求a的取值范围。
是减函数,如果p或q为真,p且q为假,求a的取值范围。
(3)在(2)的条件下,比较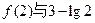 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com