
 如图,现有一块矩形空地,要在这块空地上开辟一个内
如图,现有一块矩形空地,要在这块空地上开辟一个内 接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知
接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知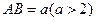 ,
,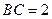 ,且
,且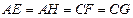 ,设
,设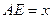 ,绿地面积为
,绿地面积为 .
.
1、写出 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
2、当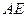 为何值时,绿地面积
为何值时,绿地面积 最大?
最大?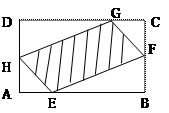
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
函数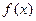 满足:①定义域是
满足:①定义域是 ; ②当
; ②当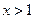 时,
时,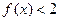 ;
;
③对任意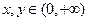 ,总有
,总有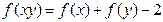
(1)求出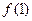 的值;
的值;
(2)判断函数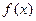 的单调性,并用单调性的定义证明你的结论;
的单调性,并用单调性的定义证明你的结论;
(3)写出一个满足上述条件的具体函数。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若二次项系数为a的二次函数 同时满足如下三个条件,求
同时满足如下三个条件,求 的解析式.
的解析式.
①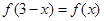 ;②
;② ;③对任意实数
;③对任意实数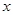 ,都有
,都有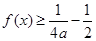 恒成立.
恒成立.
(文) 设二次函数 满足:(1)
满足:(1)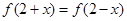 ,(2)被
,(2)被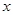 轴截得的弦长为2,(3)在
轴截得的弦长为2,(3)在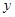 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某自来水厂的蓄水池中有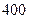 吨水,每天零点开始向居民供水,同时以每小时
吨水,每天零点开始向居民供水,同时以每小时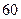 吨的速度向池中注水.已知
吨的速度向池中注水.已知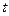 小时内向居民供水总量为
小时内向居民供水总量为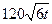 吨
吨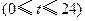 ,问
,问
(1)每天几点时蓄水池中的存水量最少?
(2)若池中存水量不多于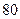 吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分 ) .已知函数y=
) .已知函数y= f(x)=
f(x)=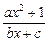 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<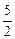
(1)试求函数f(x)的解析式
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说 明理由.
明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com