
若二次项系数为a的二次函数 同时满足如下三个条件,求
同时满足如下三个条件,求 的解析式.
的解析式.
①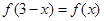 ;②
;② ;③对任意实数
;③对任意实数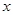 ,都有
,都有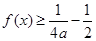 恒成立.
恒成立.
(文) 设二次函数 满足:(1)
满足:(1)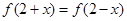 ,(2)被
,(2)被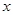 轴截得的弦长为2,(3)在
轴截得的弦长为2,(3)在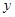 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)某商品在近30天内每件的销售价格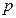 (元)与时间
(元)与时间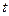 (天)的函数关系是
(天)的函数关系是 该商品的日销售量
该商品的日销售量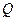 (件)与时间
(件)与时间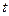 (天)的函数关系是
(天)的函数关系是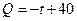
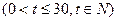 ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几 天?
天?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,现有一块矩形空地,要在这块空地上开辟一个内
如图,现有一块矩形空地,要在这块空地上开辟一个内 接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知
接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知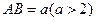 ,
,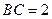 ,且
,且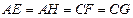 ,设
,设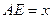 ,绿地面积为
,绿地面积为 .
.
1、写出 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
2、当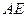 为何值时,绿地面积
为何值时,绿地面积 最大?
最大?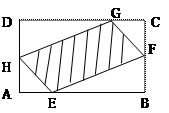
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情 况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:
况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明: 当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函数v(x)的表达式.
当20≤x≤200时,车流速度v是车流密度x的一次函数.当0≤x≤200时,求函数v(x)的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com