
某自来水厂的蓄水池中有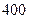 吨水,每天零点开始向居民供水,同时以每小时
吨水,每天零点开始向居民供水,同时以每小时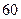 吨的速度向池中注水.已知
吨的速度向池中注水.已知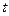 小时内向居民供水总量为
小时内向居民供水总量为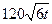 吨
吨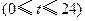 ,问
,问
(1)每天几点时蓄水池中的存水量最少?
(2)若池中存水量不多于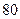 吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护需50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某商品在近30天内每件的销售价格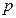 (元)与时间
(元)与时间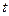 (天)的函数关系是
(天)的函数关系是 该商品的日销售量
该商品的日销售量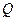 (件)与时间
(件)与时间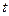 (天)的函数关系是
(天)的函数关系是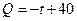
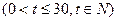 ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几 天?
天?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,现有一块矩形空地,要在这块空地上开辟一个内
如图,现有一块矩形空地,要在这块空地上开辟一个内 接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知
接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知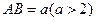 ,
,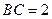 ,且
,且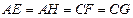 ,设
,设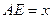 ,绿地面积为
,绿地面积为 .
.
1、写出 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
2、当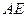 为何值时,绿地面积
为何值时,绿地面积 最大?
最大?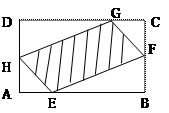
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知函数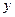 =
=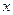 +
+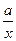 有如下性质:如果常数
有如下性质:如果常数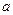 >0,那么该
>0,那么该
函数在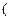 0,
0,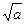
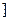 上是减函数,在
上是减函数,在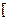
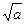 ,+∞
,+∞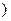 上是增函数.
上是增函数.
(1)如果函数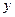 =
=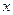 +
+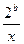 (
(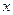 >0)的值域为
>0)的值域为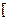 6,+∞
6,+∞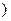 ,求
,求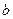 的值;
的值;
(2)研究函数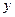 =
=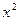 +
+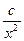 (常数
(常数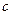 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数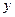 =
=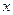 +
+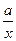 和
和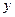 =
=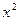 +
+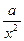 (常数
(常数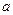 >0)作出推广,使它们都是你所推广的
>0)作出推广,使它们都是你所推广的
函数的特例.
(4)(理科生做)研究推广后的函数的单调性(只须写出结论,不必证明),并求函数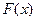 =
=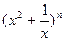 +
+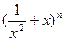 (
(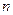 是正整数)在区间[
是正整数)在区间[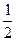 ,2]上的最大值和最小值(可利用你
,2]上的最大值和最小值(可利用你
的研究结论).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数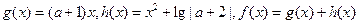 ,其中
,其中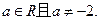
(1)若 为偶函数,求a的值;
为偶函数,求a的值;
(2)命题p:函数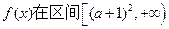 上是增函数,命题q:函数
上是增函数,命题q:函数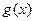 是减函数,如果p或q为真,p且q为假,求a的取值范围。
是减函数,如果p或q为真,p且q为假,求a的取值范围。
(3)在(2)的条件下,比较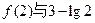 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com