
 的展开式中,第5项的系数与第3项的系数之比是56:3.
的展开式中,第5项的系数与第3项的系数之比是56:3. 的值.
的值.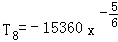 ,(3)
,(3)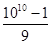 .
.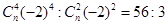 解得n=10,因为通项:
解得n=10,因为通项: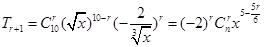 ,当5﹣
,当5﹣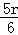 为整数,r可取0,6,于是有理项为T1=x5和T7=13400,(2)求展开式中系数绝对值最大的项,通过列不等式解决. 设第r+1项系数绝对值最大,则
为整数,r可取0,6,于是有理项为T1=x5和T7=13400,(2)求展开式中系数绝对值最大的项,通过列不等式解决. 设第r+1项系数绝对值最大,则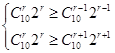 ,解得
,解得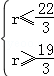 ,于是r只能为7,所以系数绝对值最大的项为
,于是r只能为7,所以系数绝对值最大的项为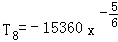 ,(3)本题是二项式定理的逆向应用,关键将式子转化符合二项展开式的特征.
,(3)本题是二项式定理的逆向应用,关键将式子转化符合二项展开式的特征. 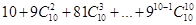
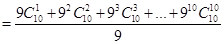
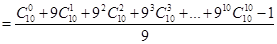
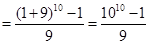
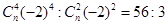 解得n=10 (2分)
解得n=10 (2分)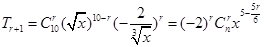 (3分)
(3分)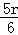 为整数,r可取0,6 (4分)
为整数,r可取0,6 (4分)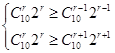 (8分)
(8分) ,于是r只能为7 (10分)
,于是r只能为7 (10分)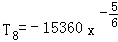 (11分)
(11分)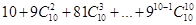
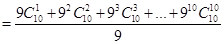
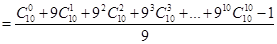 13分
13分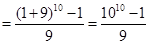 .16分
.16分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com