
分析 由条件利用三角恒等变换化简函数f(x)的解析式,再利用正弦函数的定义域和值域求得f(x)的值域.
解答 解:(1)由于$f(x)=2sinx•cos({x+\frac{π}{3}})+\frac{{\sqrt{3}}}{2}=sinxcosx-\sqrt{3}{sin^2}x+\frac{{\sqrt{3}}}{2}=sin({2x+\frac{π}{3}})$.
∴$f({-\frac{π}{4}})=sin({-\frac{π}{6}})=-\frac{1}{2}$.
(2)∵$x∈[{0,\frac{π}{2}}]$,∴$2x+\frac{π}{3}∈[{\frac{π}{3},\frac{4π}{3}}]$,∴$f(x)∈[{-\frac{{\sqrt{3}}}{2},1}]$.
点评 本题主要考查三角恒等变换,正弦函数的定义域和值域,属于基础题.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2012}{2011}$ | B. | $\frac{2010}{2011}$ | C. | $\frac{2013}{2012}$ | D. | $\frac{2011}{2012}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S中没有人认识S中所有的人 | B. | S中至多有2人认识S中所有的人 | ||
| C. | S中至多有2人不认识S中所有的人 | D. | S中至少有1人认识S中的所有人 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
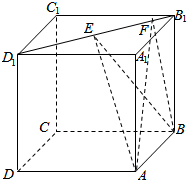 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com