
【题目】已知函数f(x)=ax+b(a>0,a≠1)满足f(x+y)=f(x)f(y),且f(3)=8.
(1)求实数a,b的值;
(2)若不等式|x﹣1|<m的解集为(b,a),求实数m的值.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】将函数y=2cos(x﹣ ![]() )的图象上所有的点的横坐标缩短到原来的
)的图象上所有的点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),得到函数y=g(x)的图象,则函数y=g(x)的图象( )
倍(纵坐标不变),得到函数y=g(x)的图象,则函数y=g(x)的图象( )
A.关于点(﹣ ![]() ,0)对称
,0)对称
B.关于点( ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是椭圆 ![]() =1的左、右焦点.
=1的左、右焦点.
(1)若M是该椭圆上的一点,且∠F1MF2=120°,求△F1MF2的面积;
(2)若P是该椭圆上的一个动点,求 ![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的一个焦点与抛物线y2=8x的焦点重合,点
的一个焦点与抛物线y2=8x的焦点重合,点 ![]() 在C上.
在C上.
(1)求椭圆C的方程;
(2)若椭圆C的一条弦被M(2,1)点平分,求这条弦所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.如果两条直线l1与l2垂直,那么它们的斜率之积一定等于﹣1
B.“a>0,b>0”是“ ![]() +
+ ![]() ≥2”的充分必要条件
≥2”的充分必要条件
C.命题“若x=y,则sinx=siny”的逆否命题为真命题
D.“a≠﹣5或b≠5”是“a+b≠0”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
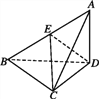
(1)求证:平面ABC⊥平面ACD;
(2)若E为AB中点,求点A到平面CED的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x+2sin2x+2sinx.
(1)将函数f(2x)的图象向右平移![]() 个单位得到函数g(x)的图象,若x∈
个单位得到函数g(x)的图象,若x∈![]() ,求函数g(x)的值域;
,求函数g(x)的值域;
(2)已知a,b,c分别为△ABC中角A,B,C的对边,且满足f(A)=![]() +1,A∈
+1,A∈![]() ,a=2
,a=2![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足:a1=1,an+1=3an , n∈N* . 设Sn为数列{bn}的前n项和,已知b1≠0,2bn﹣b1=S1Sn , n∈N*(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bnlog3an , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥底面ABCD, ![]() ,PA=2,E是PC上的一点,PE=2EC.
,PA=2,E是PC上的一点,PE=2EC.
(Ⅰ)证明:PC⊥平面BED;
(Ⅱ)设二面角A﹣PB﹣C为90°,求PD与平面PBC所成角的大小.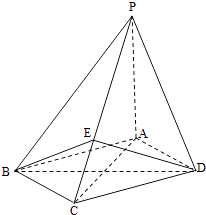
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com